Comparative study of deep learning models for daily karst spring discharge forecasting: LSTM Versus Hybrid VMD–LSTM
-
摘要: 岩溶泉流量具有强非平稳与多尺度耦合特征，给精确预测带来挑战。为同时提升预测精度与物理可解释性，文章提出将变分模态分解（VMD）与长短期记忆网络（LSTM）耦合的 VMD-LSTM 框架：先用 VMD 将泉流量序列分解为若干本征模态，再与降雨共同作为输入，驱动两层 LSTM 进行建模；并以标准 LSTM 为基线开展对比评估。以桂林寨底岩溶系统 2013—2023 年日尺度数据为研究对象，VMD-LSTM 在训练、验证与测试阶段均优于基线模型；其中测试期达到纳什效率系数=0.951、均方根误差=0.524，且峰值均方根误差（观测前5%）下降 75.2%，显著增强了对极端事件的刻画能力。结果表明：VMD 可有效缓解原序列的非平稳与模态混叠，使 LSTM 更稳定地捕捉“快响应—慢退水”的动力学过程。该方法对岩溶区洪水预警与水资源调度具有现实应用价值。Abstract:
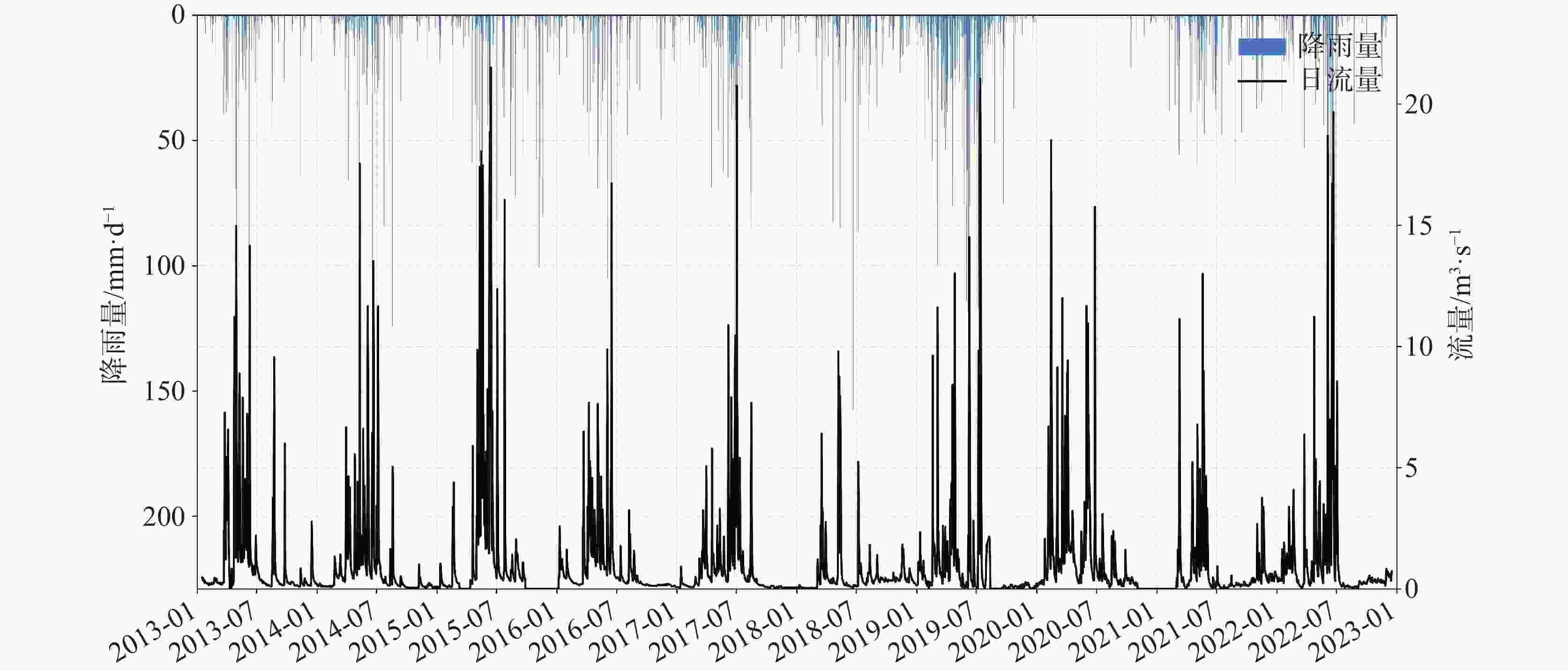
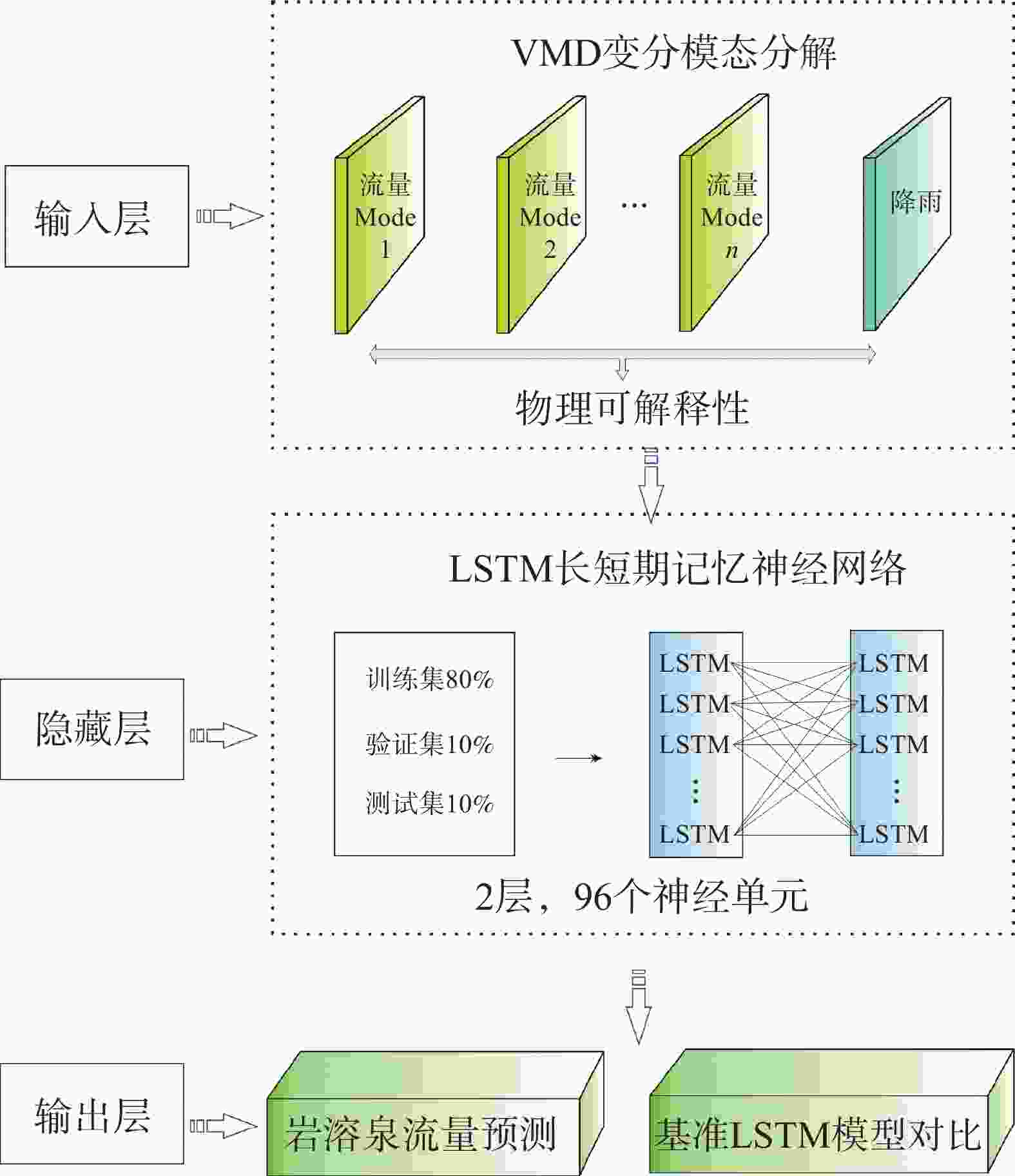
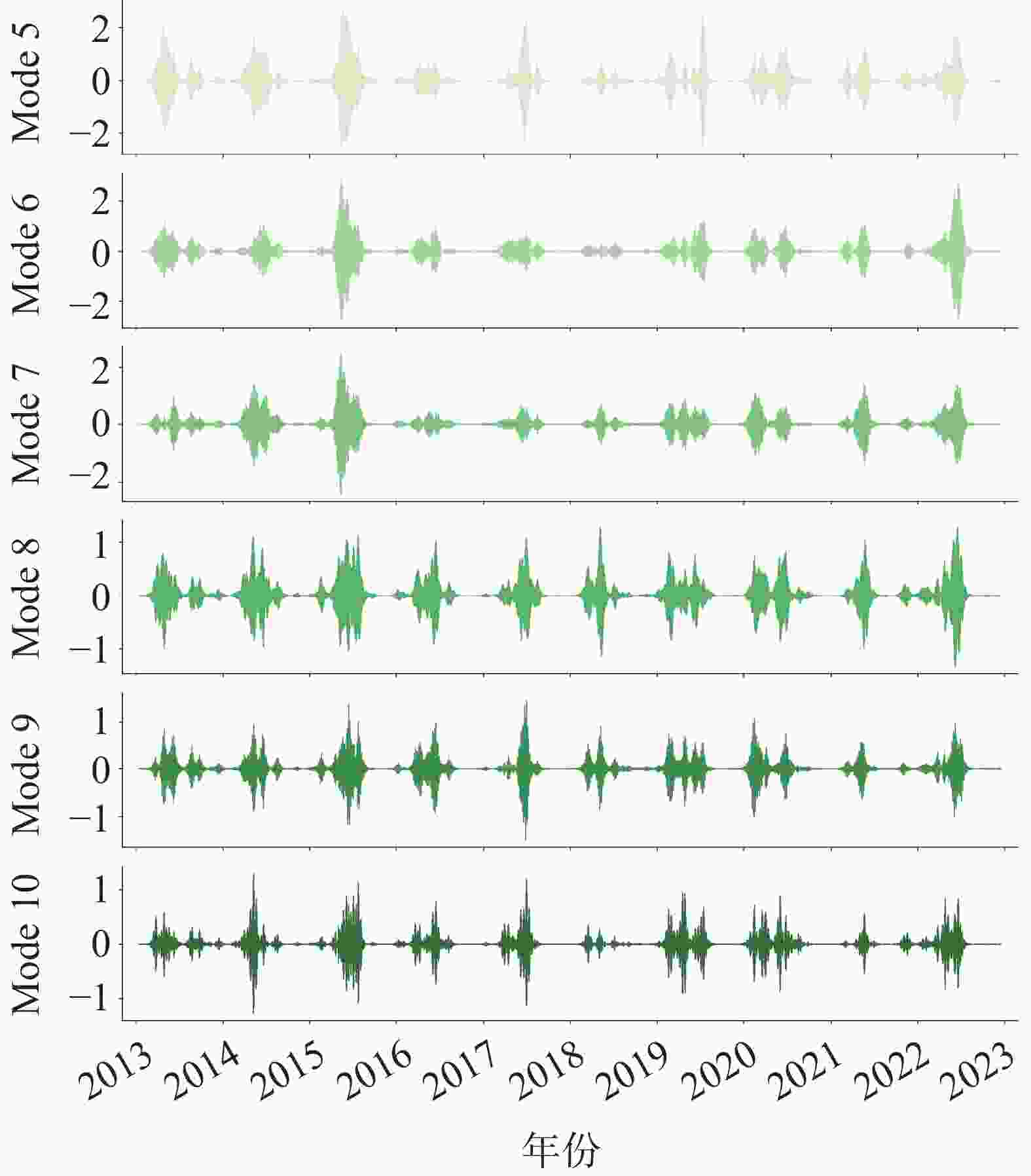
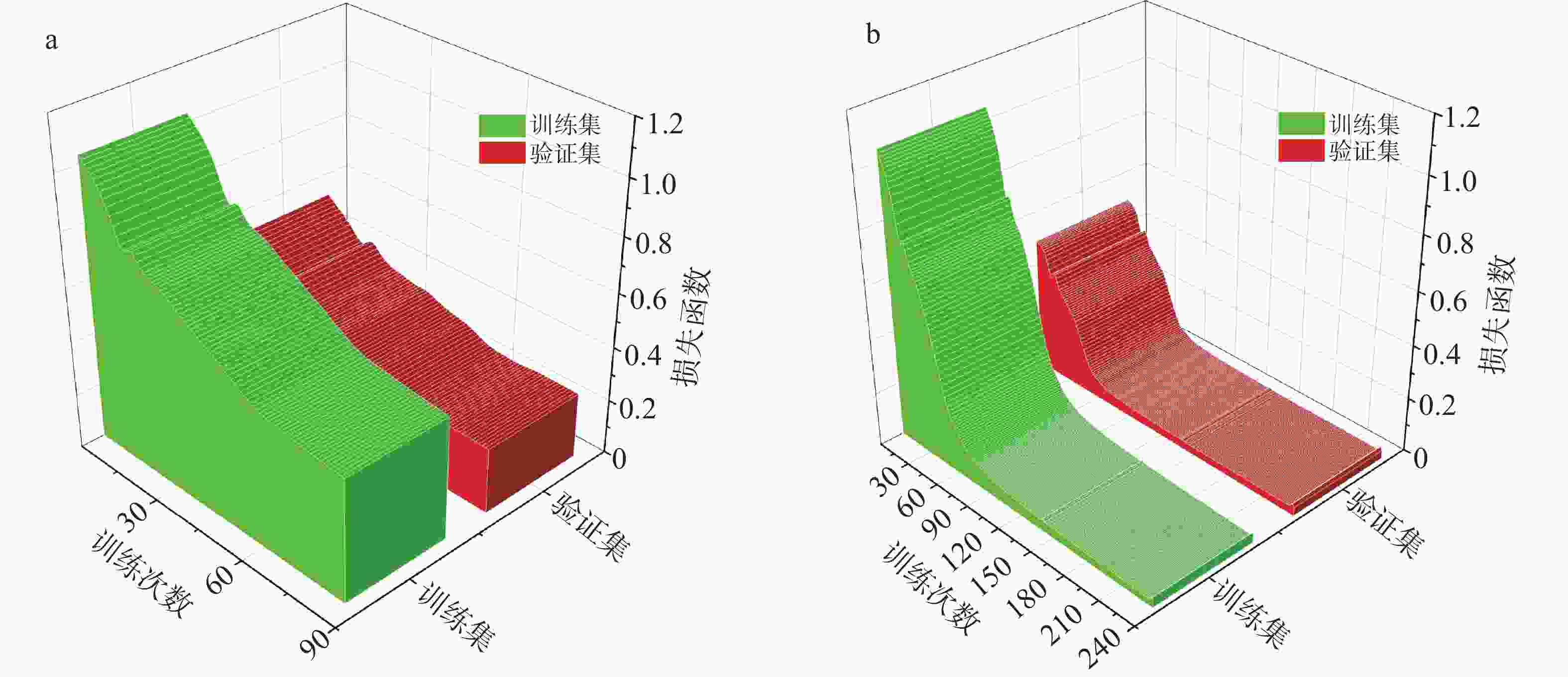
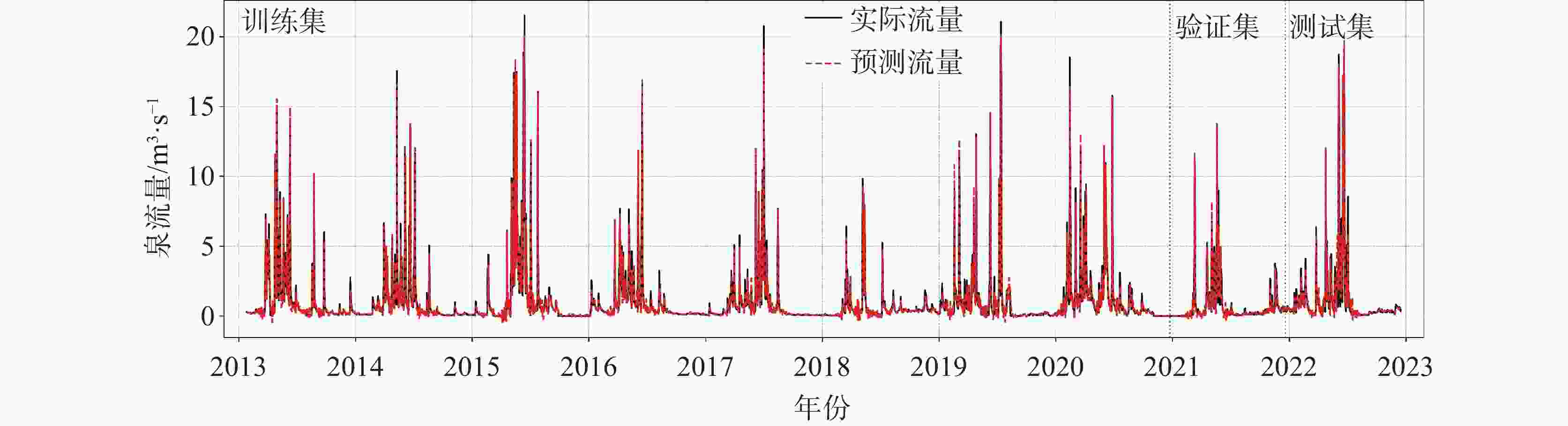
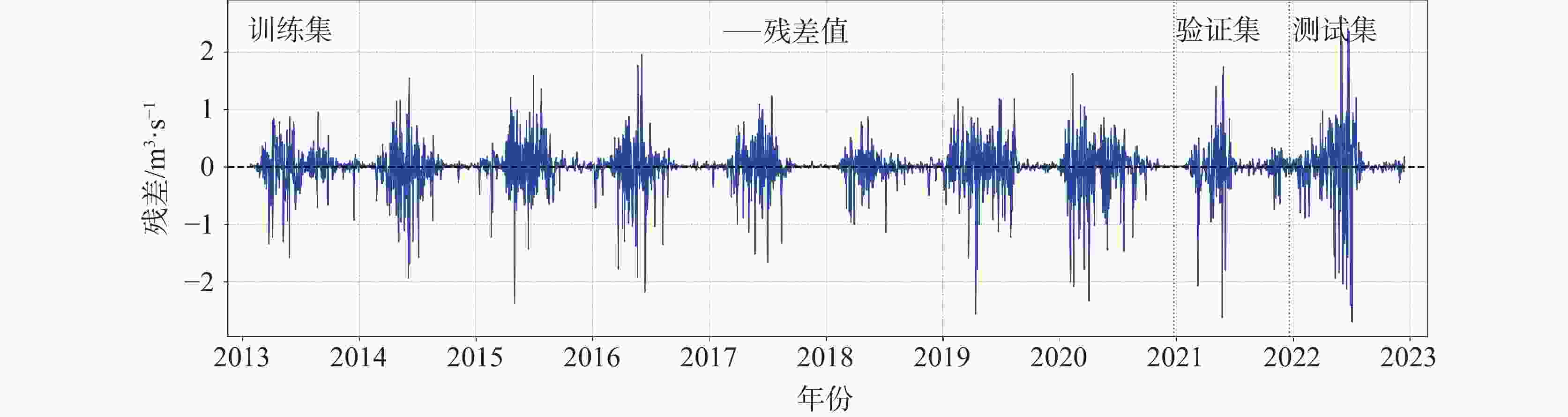
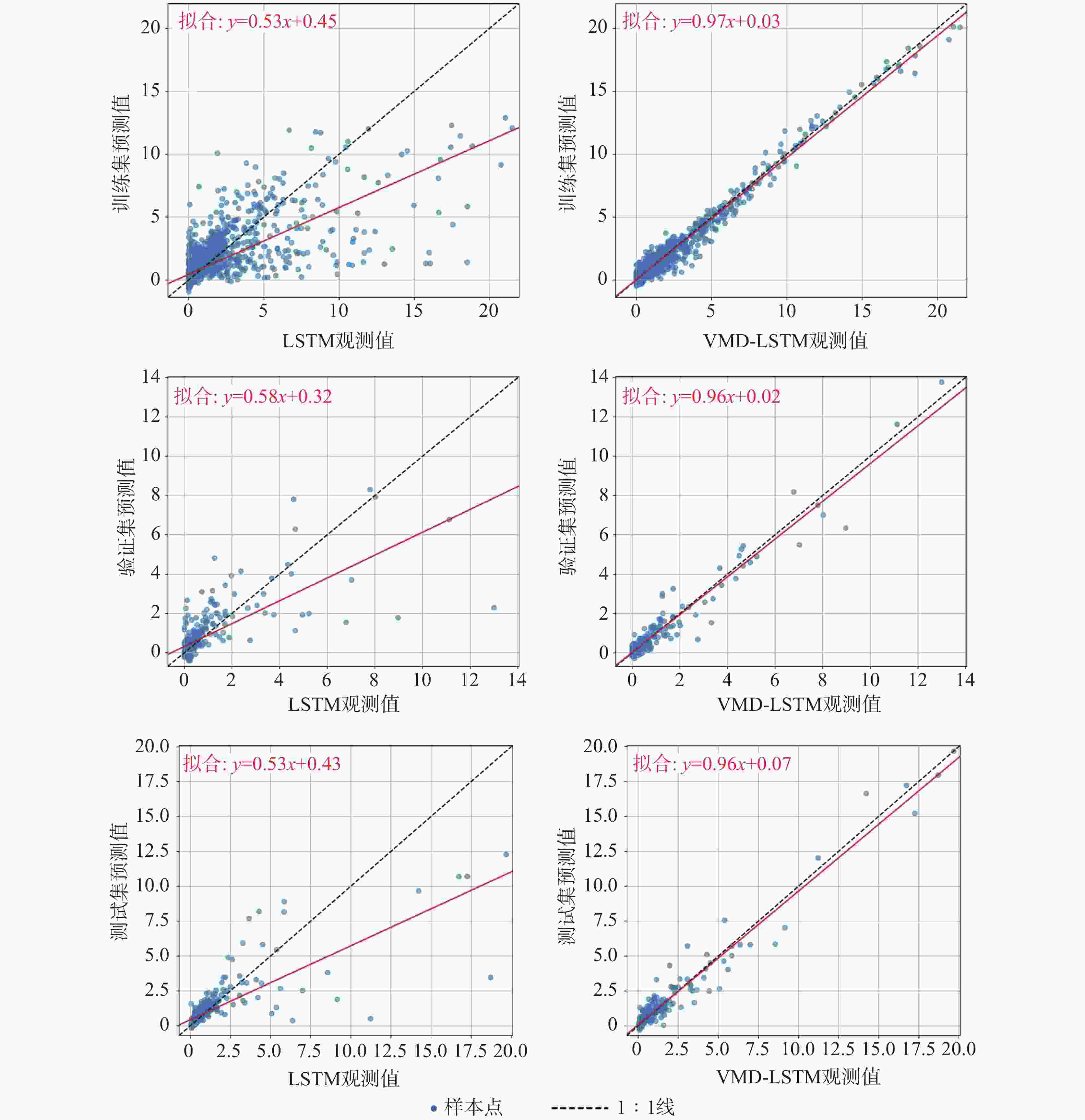
The discharge process of karst spring is controlled by complex hydrogeological structure and multi-scale dynamic mechanisms,exhibits characteristics of non-stationary and strongly nonlinearity, posing significant challenges for high-precision predictive modelings. Conventional physics-based models rely heavily on extensive hydrogeological parameters and often struggle to accurately capture non-stationary processes during extreme events. Consequently,integrating signal decomposition techniques with deep learning has emerged as a promising approach to enhance both prediction accuracy and physical interpretability. This study develops a hybrid model that combines Variational Mode Decomposition (VMD) with a Long-Short-Term Memory (LSTM) networks, referred to as VMD-LSTM, aiming to address non-stationarity and multi-scale coupling issues in daily karst spring discharge forecasting. Through a system comparison of the performance of the VMD-LSTM model and standard LSTM model during training, validation, and testing phases, the study evaluates improvements in prediction accuracy, extreme events characterization, and model stability, while elucidating the mechanisms by which VMD enhances the modeling performance of LSTM. This study utilized daily spring discharge and corresponding precipitation data from the Zhaidi karst system in Guilin, Guangxi, spanning from 2013 to 2023. The original spring discharge series was decomposed using VMD into ten Intrinsic Mode Functions (IMFs). Among them,six modes(Mode 5 to Mode10), which collectively represent the dominant karst hydrodynamic processes, were selected as inputs to a two-layer LSTM network for modeling. The model was trained using the Adam optimizer and the mean squared error loss function. The dataset was chronologically partitioned into a training set (80%), a validation set (10%), and a testing set (10%). Model performance was comprehensively evaluated using metrics including RMSE, MAE, NSE, KGE, and peak RMSE (caculated for the top 5% of high-flow events). Results demonstrated that the VMD-LSTM model consistently outperformed the standard LSTM across all three phases of the training,validation and testing. During the testing phase, the VMD-LSTM achieved an NSE of 0.951 and an RMSE of 0.524, representing improvements of 57.0% and 64.6%, respectively, compared to the LSTM model. Notably, the hybrid model exhibited substantially enhanced capability in predicting extreme discharges, reducing the peak RMSE from 6.208 to 1.542(a decrease of 75.2%). The VMD decomposition effectively mitigated non-stationarity and mode mixing present in the original series, enabling the LSTM network to more reliably identify and simulate the "rapid response–slow recession" characteristcs inherent in karst hydrological processes. This approach significantly syppressed the systematic underestimation and error dispersion during high-flow events. The VMD-LSTM hybrid model not only markedly enhanced the forecasting accuracy and extreme event modeling for karst spring discharge but also exhibited strong cross-phase consistency and physical interpretability, demonstrating high generalizability and robustness in practical forecasting scenarios. Future research could focus on incorporating hydrological physical constraints, conducting uncertainty quantification analysis, and extending the framework to higher spatiotemporal resolutions and multivariable coupling to further enhance model applicability and forcasting reliability across diverse karst systems. -
图 1 寨底岩溶地下河系统水文地质简图
Figure 1. Hydrogeological sketch map of the Zhaidi karst underground river system
图 2 寨底岩溶地下河系统泉流量与降雨时间序列（2013-2023）
Figure 2. Time series of spring discharge and precipitation in the Zhaidi karst underground river system (from 2013 to 2023)
图 5 泉流量分解Mode 5-10模态函数
Figure 5. Spring discharge decomposition mode(mode 5 to mode 10) into Intrinsic Mode Functions (IMFs)
图 6 训练期和验证期损失函数(a.LSTM模型, b.VMD-LSTM模型)
Figure 6. Loss functions of training phase and validation phase(a.LSTM, b.VMD-LSTM)
图 7 不同时段流量预测对比
Figure 7. Comparison of discharge forecasting across representative periods
图 8 VMD-LSTM不同阶段流量预测残差图
Figure 8. Residuals of VMD−LSTM discharge forecasting across different phases
图 9 不同模型流量模拟值与观测值对比（训练集、验证集、测试集）
Figure 9. Comparison of simulated versus observed discharge values for different models( training sets, validation sets, and testing sets)
图 10 不同模拟期典型丰水期、枯水期对比
Figure 10. Comparison of typical high-flow and low-flow periods across different modeling phases
图 11 LSTM 与 VMD-LSTM 模型的绝对误差与峰值误差对比
Figure 11. Comparison of absolute error and peak error between the LSTM and VMD–LSTM models
表 1 VMD变分模态分解
Table 1. Summary of VMD
模态 贡献率/% 主导周期/d 物理意义 Mode1 45.91 362.2 年际/季度趋势 Mode2 14.53 28.7 中期影响 Mode3 10.69 14.1 中期影响 Mode4 7.86 8.3 中期影响 Mode5 6.94 5.1 短期响应 Mode6 5.15 4.1 短期响应 Mode7 3.56 3.8 短期响应 Mode8 2.35 3.2 短期响应 Mode9 1.67 2.6 降雨—补给事件 Mode10 1.35 2.2 降雨—补给事件 
下载: 导出CSV
表 2 LSTM(i)与VMD-LSTM(ii)模型结果对比
Table 2. Comparison of the results from the LSTM (i) and VMD-LSTM (ii) models
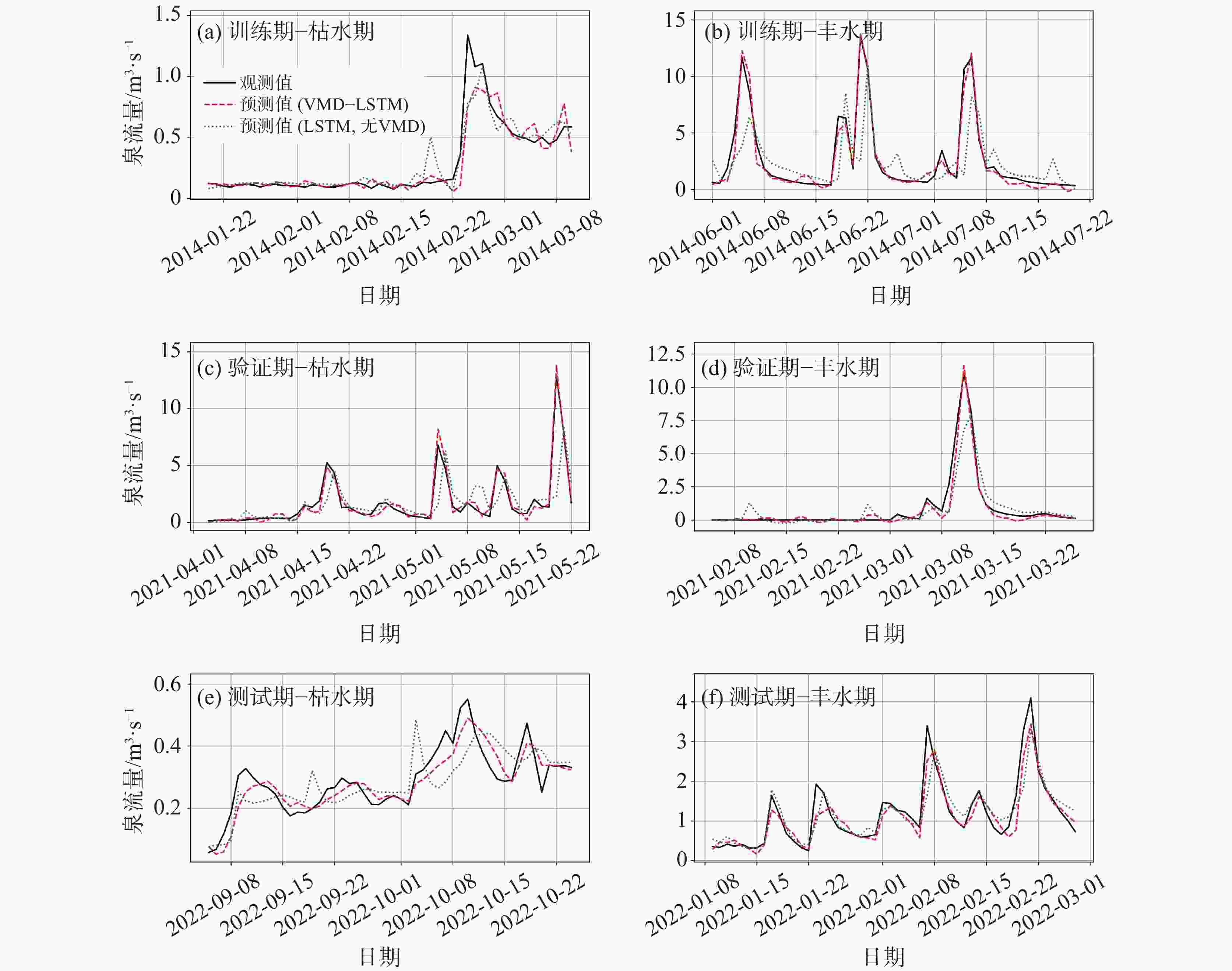
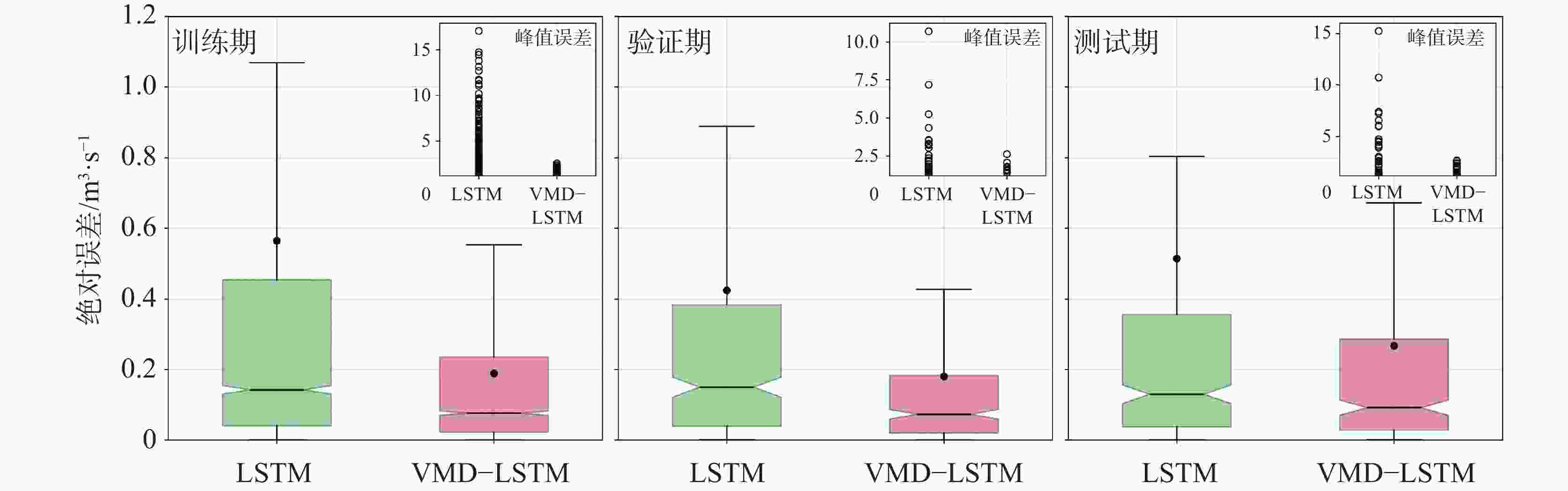
LSTM VMD-LSTM 训练期 (i) 验证期 (i) 测试期(i) 训练期(ii) 验证期(ii) 测试期(ii) RMSE 1.458 1.024 1.482 0.339 0.357 0.524 MAE 0.565 0.425 0.515 0.189 0.181 0.267 NSE 0.532 0.512 0.606 0.975 0.941 0.951 KGE 0.616 0.653 0.603 0.978 0.968 0.962 峰值_RMSE (5%) 5.709 3.904 6.208 0.723 1.032 1.542
下载: 导出CSV
-
[1] 王晋丽, 陈 喜, 张志才, 康建荣, 胡晋山. 基于MODFLOW的离散裂隙网络渗流分析[J]. 中国岩溶, 2025, 44(1): 1-14. doi: 10.11932/karst2024y043WANG Jinli, CHEN Xi, ZHANG Zhicai, KANG Jianrong, HU Jinshan. MODFLOW-based analysis on seepage in discrete fissure networks[J]. Carsologica Sinica, 2025, 44(1): 1-14. doi: 10.11932/karst2024y043 [2] Hartmann A, Goldscheider N, Wagener T, Lange J, Weiller W. Karst water resources in a changing world: Review of hydrological modeling approaches[J]. Reviews of Geophysics, 2014, 52(3): 218-242. doi: 10.1002/2013RG000443 [3] 赵良杰, 王莹, 周妍, 曹建文, 杨杨, 王喆. 基于 SWAT 模型的珠江流域地下水资源评价[J]. 地球科学, 2024, 49(5): 1876-1890. doi: 10.3799/dqkx.2022.004ZHAO Liangjie, WANG Ying, ZHOU Yan, CAO Jianwen, YANG Yang, WANG Zhe. Groundwater resources evaluation in the Pearl River basin based on SWAT model[J]. Earth Science, 2024, 49(5): 1876-1890. doi: 10.3799/dqkx.2022.004 [4] 杨丽, 杨广斌, 李亦秋, 李蔓. 修正SWAT模型在喀斯特小流域的径流模拟研究: 以羊鸡冲小流域为例[J]. 中国岩溶, 2024, 43(2): 291-301.YANG Li, YANG Guangbin, LI Yiqiu, LI Man. Runoff simulation of modified SWAT model in karst watershed: A case study of Yangjichong sub-watershed[J]. Carsologica Sinica, 2024, 43(2): 291-301. [5] 解子轩, 江峰, 王若帆, 吉勤克补子, 史浙明, 赵良杰. 基于GMS的岩溶地下河水流与溶质运移过程模拟研究[J]. 中国岩溶, 2025, 44(1): 57-69. doi: 10.11932/karst20250104XIE Zixuan, JIANG Feng, WANG Ruofan, JIQIN Kebuzi, SHI Zheming, ZHAO Liangjie. Simulation study of groundwater flow and solute transport processes in karst underground rivers based on GMS[J]. Carsologica Sinica, 2025, 44(1): 57-69. doi: 10.11932/karst20250104 [6] 陈喜, 刘传杰, 胡忠明, 李献昆. 泉域地下水数值模拟及泉流量动态变化预测[J]. 水文地质工程地质, 2006, 33(2): 36-40.CHEN Xi, LIU Chuanjie, HU Zhongming, LI Xiankun. Numerical modeling of groundwater in a spring catchment and prediction of variations in the spring discharge[J]. Hydrogeology & Engineering Geology, 2006, 33(2): 36-40. [7] Jourde H, Wang X. Advances, challenges and perspective in modelling the functioning of karst systems: A review[J]. Environmental Earth Sciences, 2023, 82(17): 396. doi: 10.1007/s12665-023-11034-7 [8] Chen Z, Lucianetti G, Hartmann A. Understanding groundwater storage and drainage dynamics of a high mountain catchment with complex geology using a semi-distributed process-based modelling approach[J]. Journal of Hydrology, 2023, 625: 130067. doi: 10.1016/j.jhydrol.2023.130067 [9] 邢立文, 崔宁博. 基于人工神经网络的晋祠泉水位模拟研究[J]. 人民黄河, 2019, 41(12): 63-69. doi: 10.3969/j.issn.1000-1379.2019.12.015XING Liwen, CUI Ningbo. Simulation of Jinci Spring water level on ANN Models[J]. Yellow River, 2019, 41(12): 63-69. doi: 10.3969/j.issn.1000-1379.2019.12.015 [10] Fang L, Shao D. Application of long short-term memory (LSTM) on the prediction of rainfall-runoff in karst area[J]. Frontiers in Physics, 2022, 9: 790687. [11] Vu M T, Jardani A, Massei N, Foumier M. Reconstruction of missing groundwater level data by using Long Short-Term Memory (LSTM) deep neural network[J]. Journal of Hydrology, 2021, 597(1): 125776. doi: 10.1016/j.jhydrol.2020.125776 [12] Kratzert F, Klotz D, Herrnegger M, Sampson A K, Hochreiter S, Nearing G S. Toward improved predictions in ungauged basins: Exploiting the power of machine learning[J]. Water Resources Research, 2019, 55(12): 11344-11354. doi: 10.1029/2019WR026065 [13] Gholizadeh H, Zhang Y, Frame J, Gu X, Green C T. Long short-term memory models to quantify long-term evolution of streamflow discharge and groundwater depth in Alabama[J]. Science of the Total Environment, 2023, 901: 165884. doi: 10.1016/j.scitotenv.2023.165884 [14] Le M H, Kim H, Adam S, Do H X, Beling P A, Lakshmi. Streamflow estimation in ungauged regions using machine learning: Quantifying uncertainties in geographic extrapolation[J]. Hydrology and Earth System Sciences, 2022: 1-24. [15] 马从文, 张志才, 陈喜, 程勤波, 彭韬, 张林. 基于机器学习的西南岩溶泉流量模拟研究[J]. 中国岩溶, 2024, 43(1): 48-56.MA Congwen, ZHANG Zhicai, CHEN Xi, CHENG Qinbo, PENG Tao, ZHANG Lin. Modelling karst spring flow in southwest China based on machine learning [J]. Carsologica Sinica, 2024, 43(1): 48-56. [16] Willard J, Jia X, Xu S, Steinbach M, Kumar V. Integrating scientific knowledge with machine learning for engineering and environmental systems[J]. ACM Computing Surveys, 2022, 55(4): 1-37. [17] 温忠辉, 任化准, 束龙仓, 王恩, 柯婷婷, 陈荣波. 岩溶地下河日流量预测的小样本非线性时间序列模型[J]. 吉林大学学报 (地球科学版), 2011, 41(2): 455-458.WEN Zhonghui, REN huazhun, SU Longcang, WANG En, KE Tingting, CHEN Rongbo. Daily discharge forecast of karst underground river on non-linear time series model of a small sample[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(2): 455-458. [18] 郝永红, 黄登宇, 张文忠, 王学萌. 山西神头泉流量的灰色预测模型研究[J]. 水利学报, 2004, 35(2): 111-114.HAO Yonghong, HUANG Dengyu, ZHANG Wenzhong, WANG Xuemeng. Gray prediction model for forecasting spring discharge [J]. Shuili Xuebao, 2004, 35(2): 111-114. [19] Renard B, Kavetski D, Leblois E, Thyer M, Kuczera G, Franks S W. Toward a reliable decomposition of predictive uncertainty in hydrological modeling: Characterizing rainfall errors using conditional simulation[J]. Water Resources Research, 2011, 47(11): 11516. [20] Zhou R, Wang Q, Jin A, Shi W, Liu S. Interpretable multi-step hybrid deep learning model for karst spring discharge prediction: Integrating temporal fusion transformers with ensemble empirical mode decomposition[J]. Journal of Hydrology, 2024, 645: 132235. [21] An L, Hao Y, Yeh. Simulation of karst spring discharge using a combination of singular spectrum analysis and ensemble empirical mode decomposition with LSTM modeling[J]. Environmental Earth Sciences, 2020, 79: 353. doi: 10.1007/s12665-020-09096-1 [22] Zhang S, Zhao Z, Wu J, Jin Y, Jeng D S, Li S, Li G, Ding D. Solving the temporal lags in local significant wave height prediction with a new VMD-LSTM model[J]. Ocean Engineering, 2024, 313: 119385. -
点击查看大图
计量
- 文章访问数: 385
- HTML浏览量: 269
- PDF下载量: 6
- 被引次数: 0
