Research on the mechanism and application of crystal deposition in corrugated drainage pipes
-
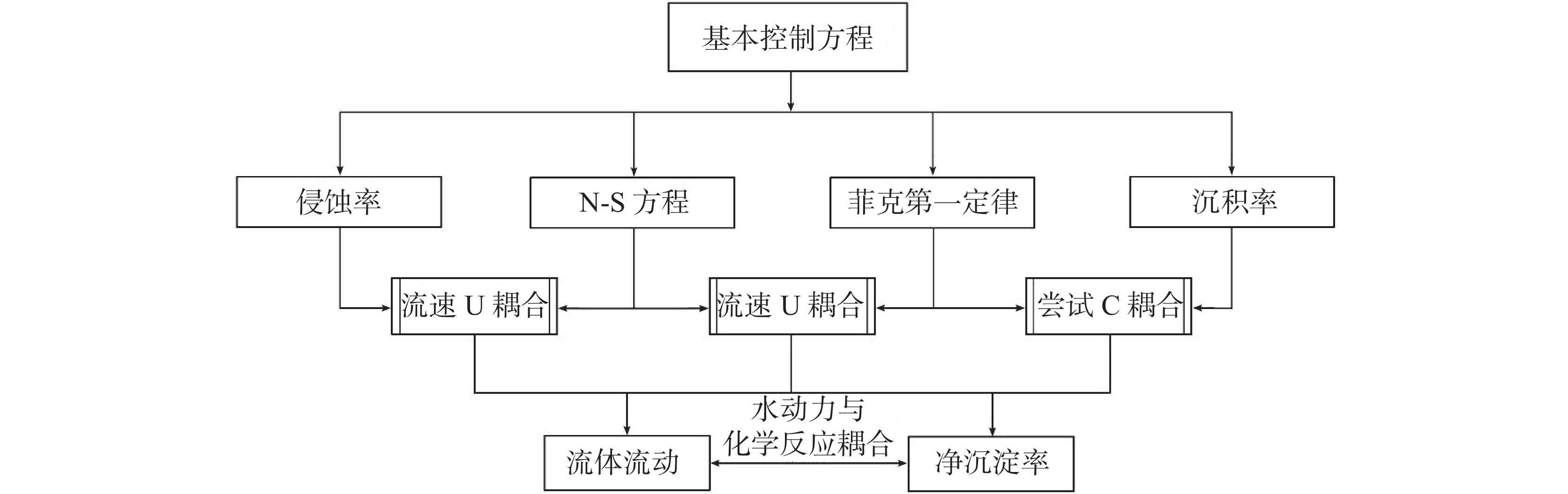
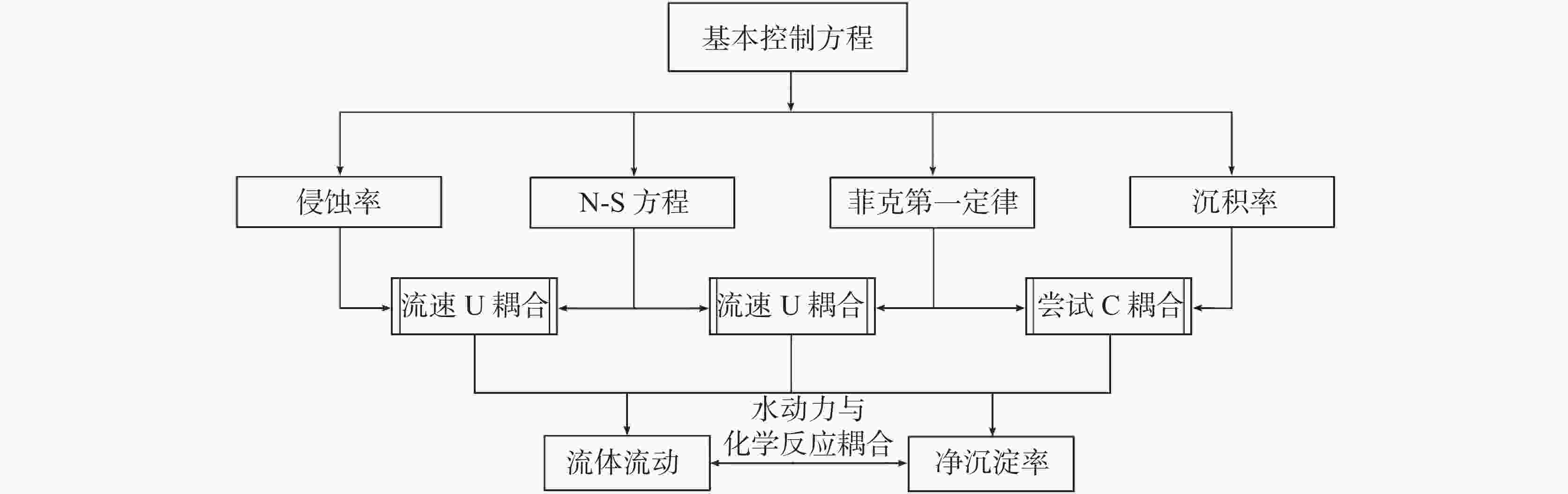
摘要: 石灰岩地区的隧道经常面临排水管淤堵问题，采用模型模拟分析排水管淤堵形成过程和影响因素较为重要。为得到能够贴合现实工况的预测模型，考虑流场与化学反应耦合，同时结合物质传递过程，构建起对波纹管类型的曲线边界的计算与模拟模型。采用相场法与动网格结合的手段得到在自由液面情况下，结晶生成同时影响诱发流场变化的过程。结果表明：该模型对内壁摩擦系数为0.2~0.3的情况有较好的准确度，摩擦系数低于0.2时，模拟则出现较大误差，原因可能是低摩擦壁面需要调整壁面函数，同时对沉积公式进行系数修正。内壁摩擦系数高于0.3的情况则因为等效砂砾粗糙度过高，失去边界层，模拟效果较差，模型不再适用。根据上述结果，将对粤北某隧道排水管的应用进行模拟，并根据模型预测的淤堵时间来进行处治，将有效预防排水管的淤堵。Abstract:
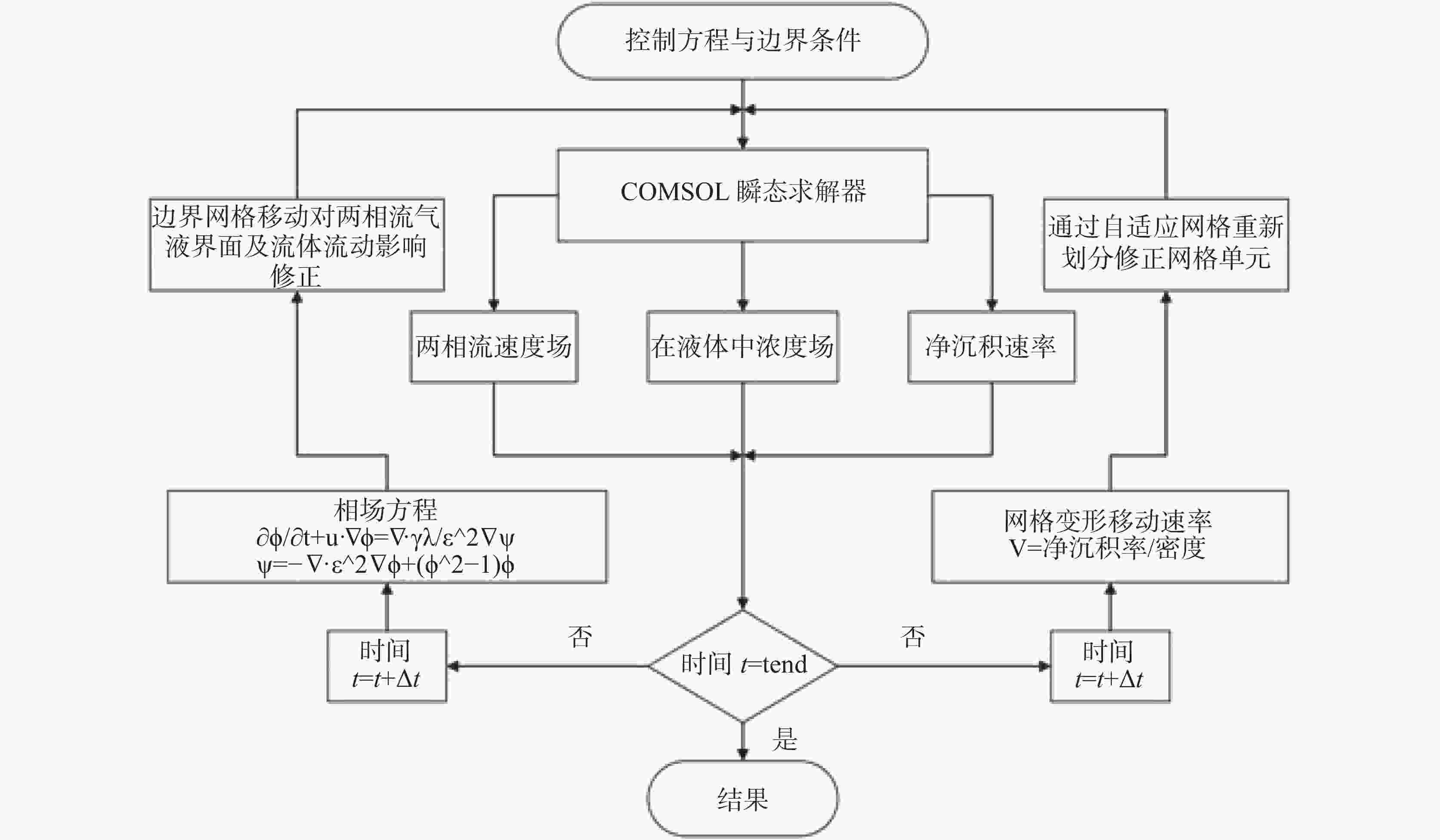
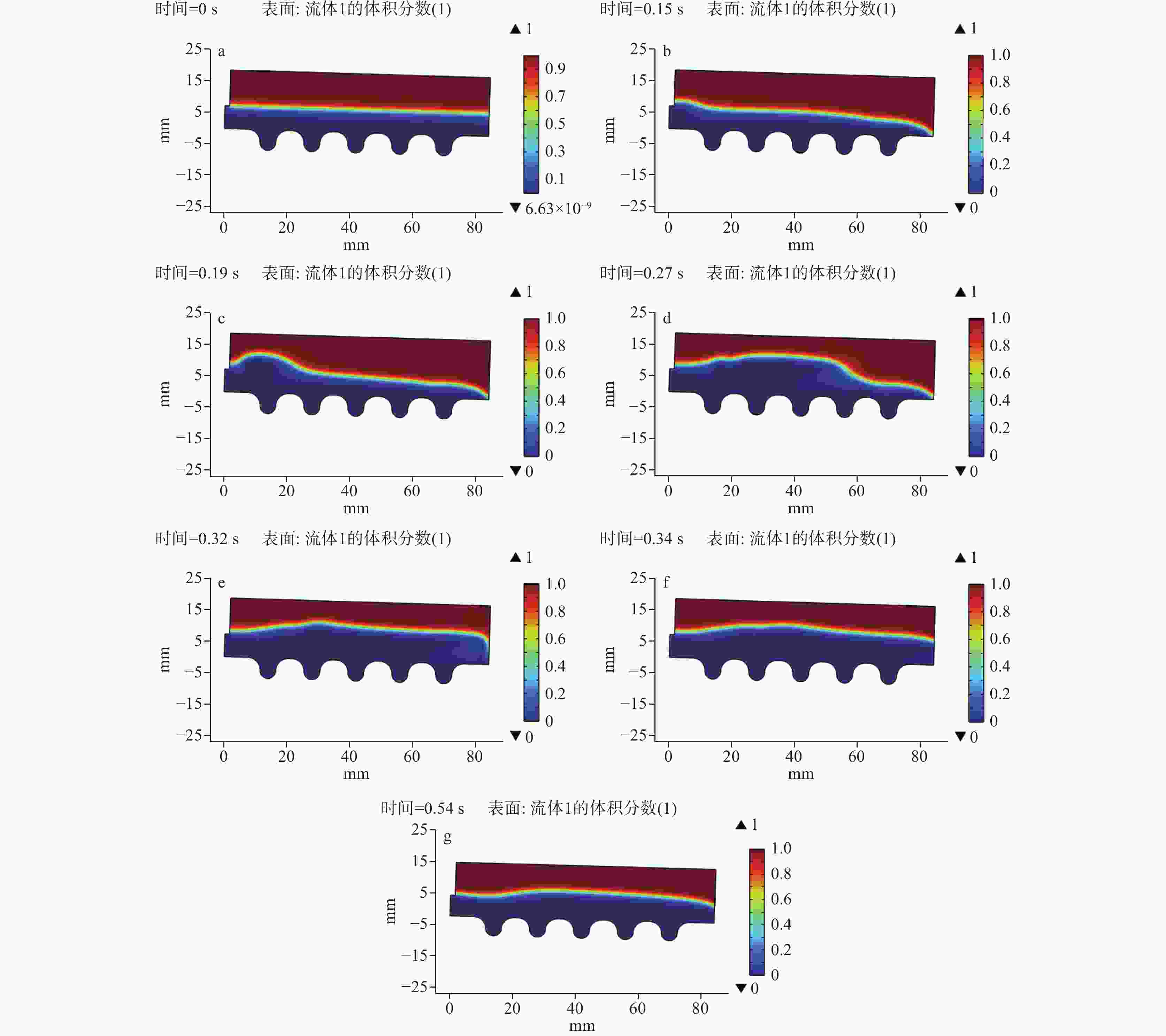
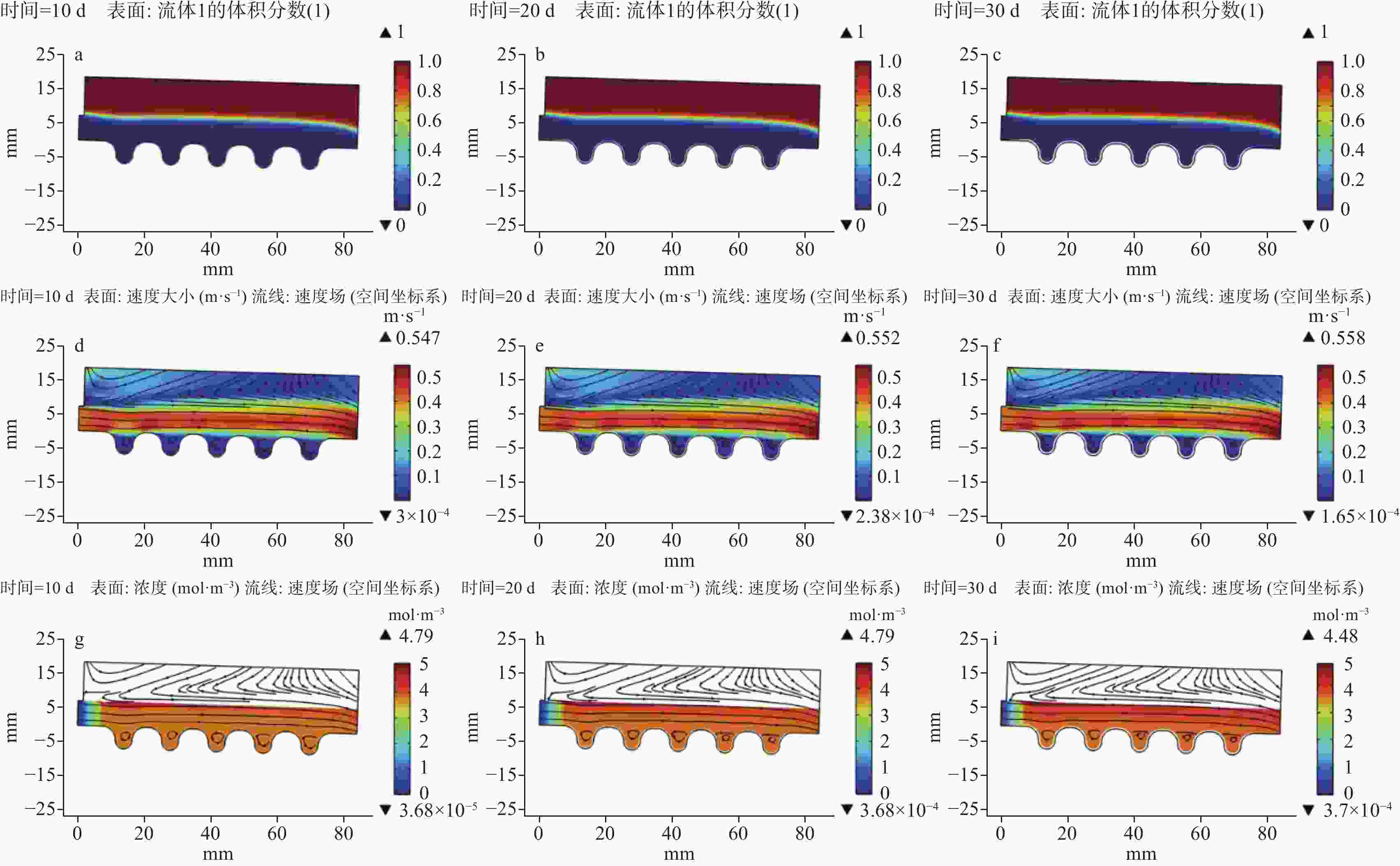
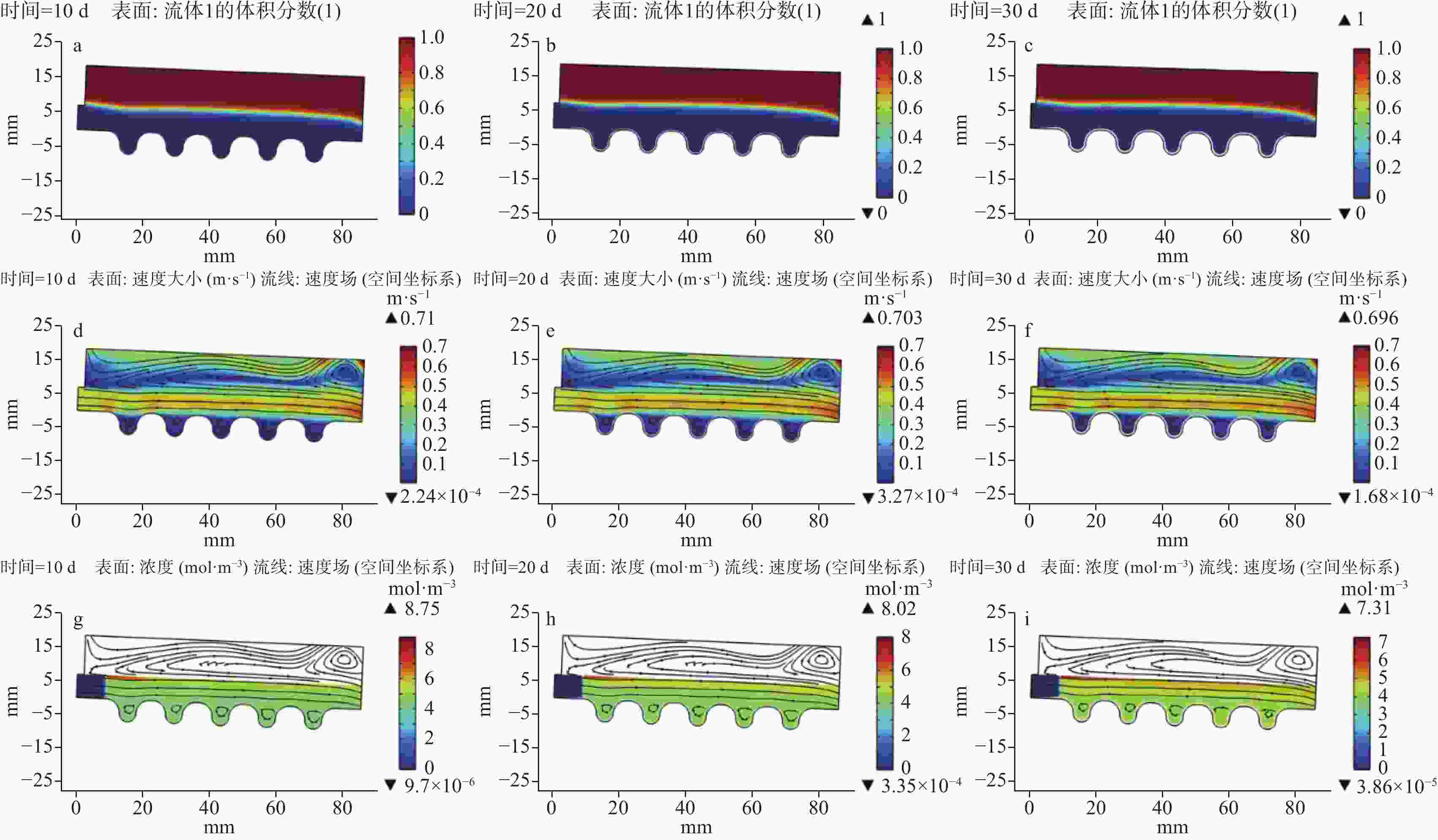
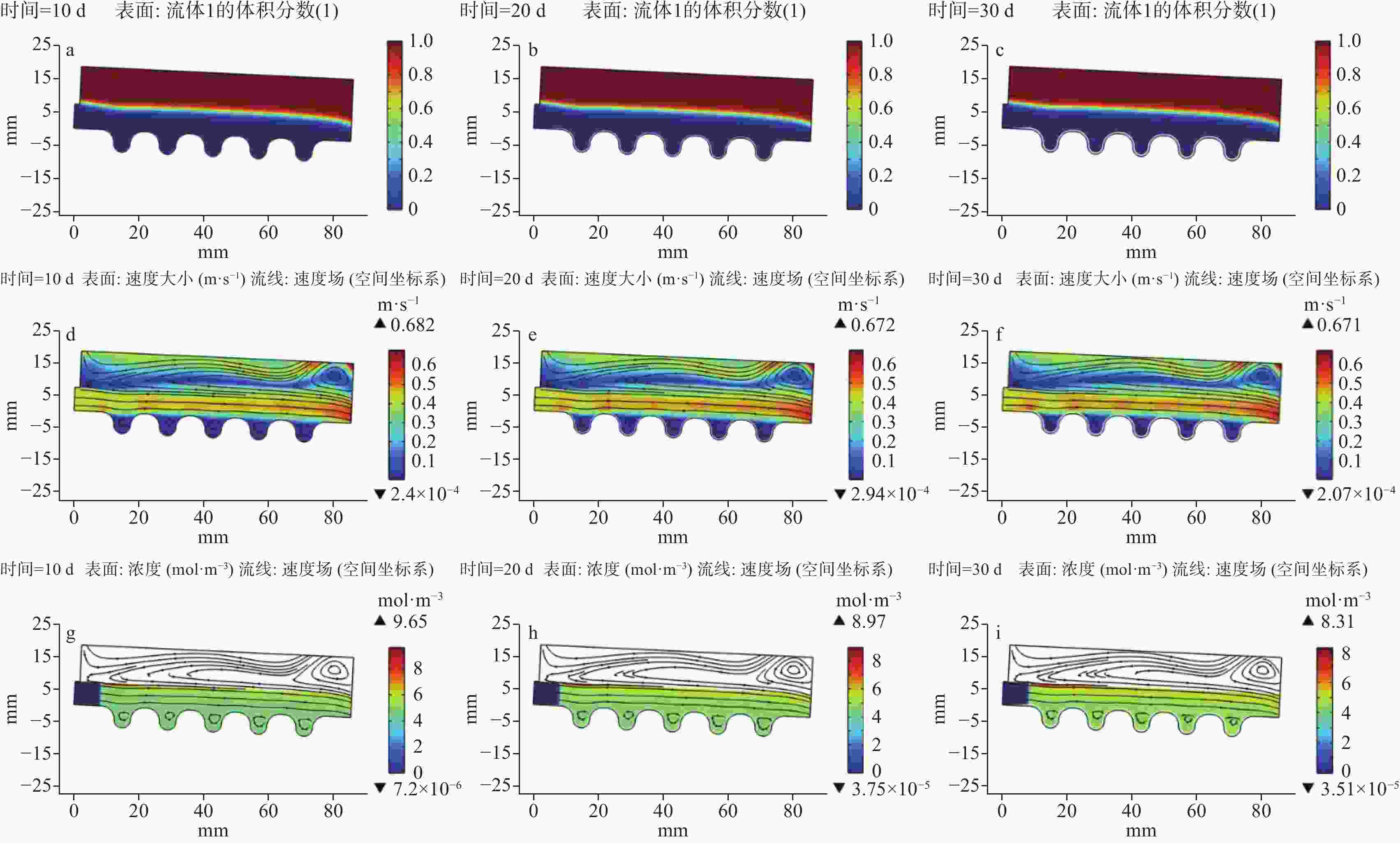
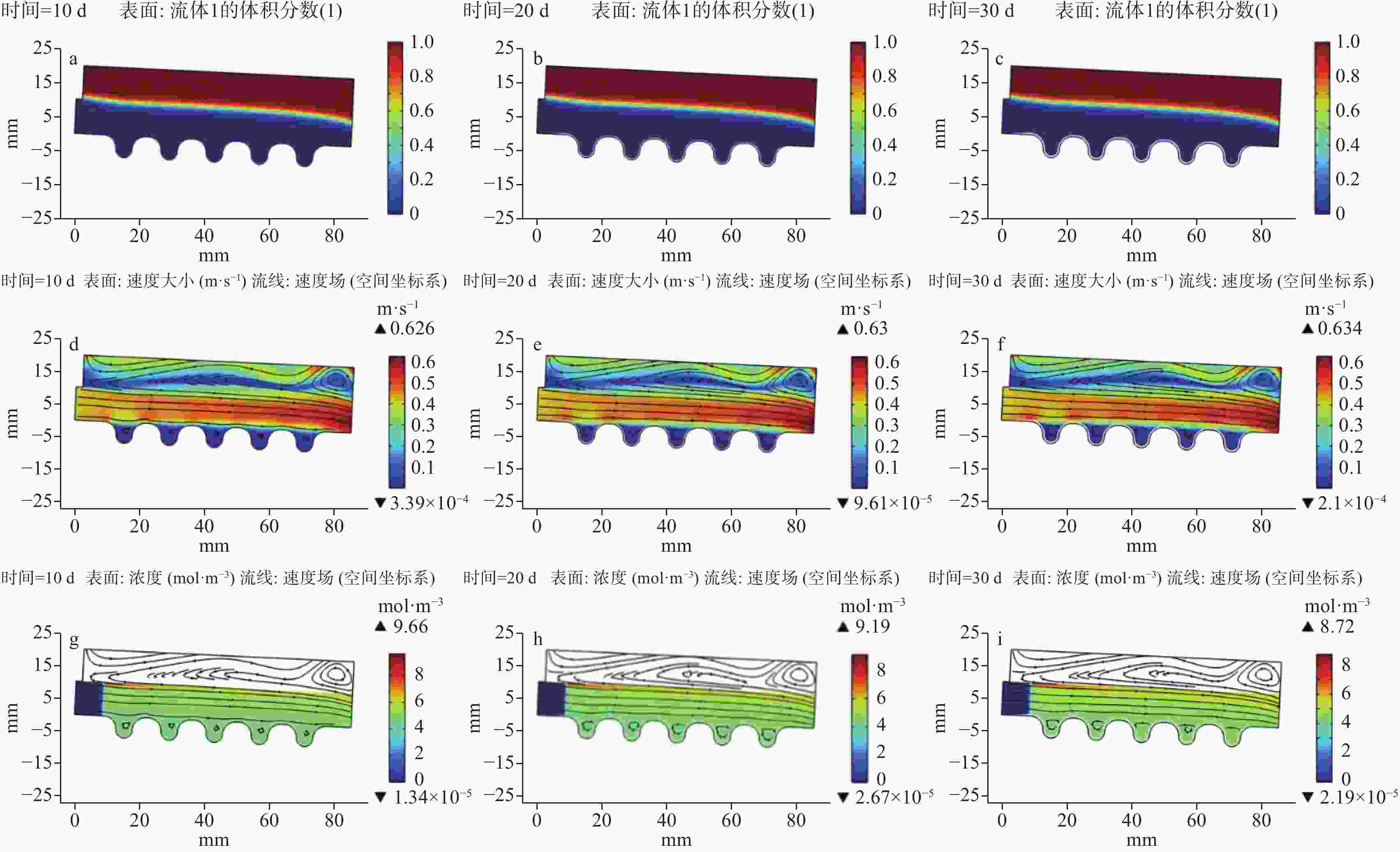
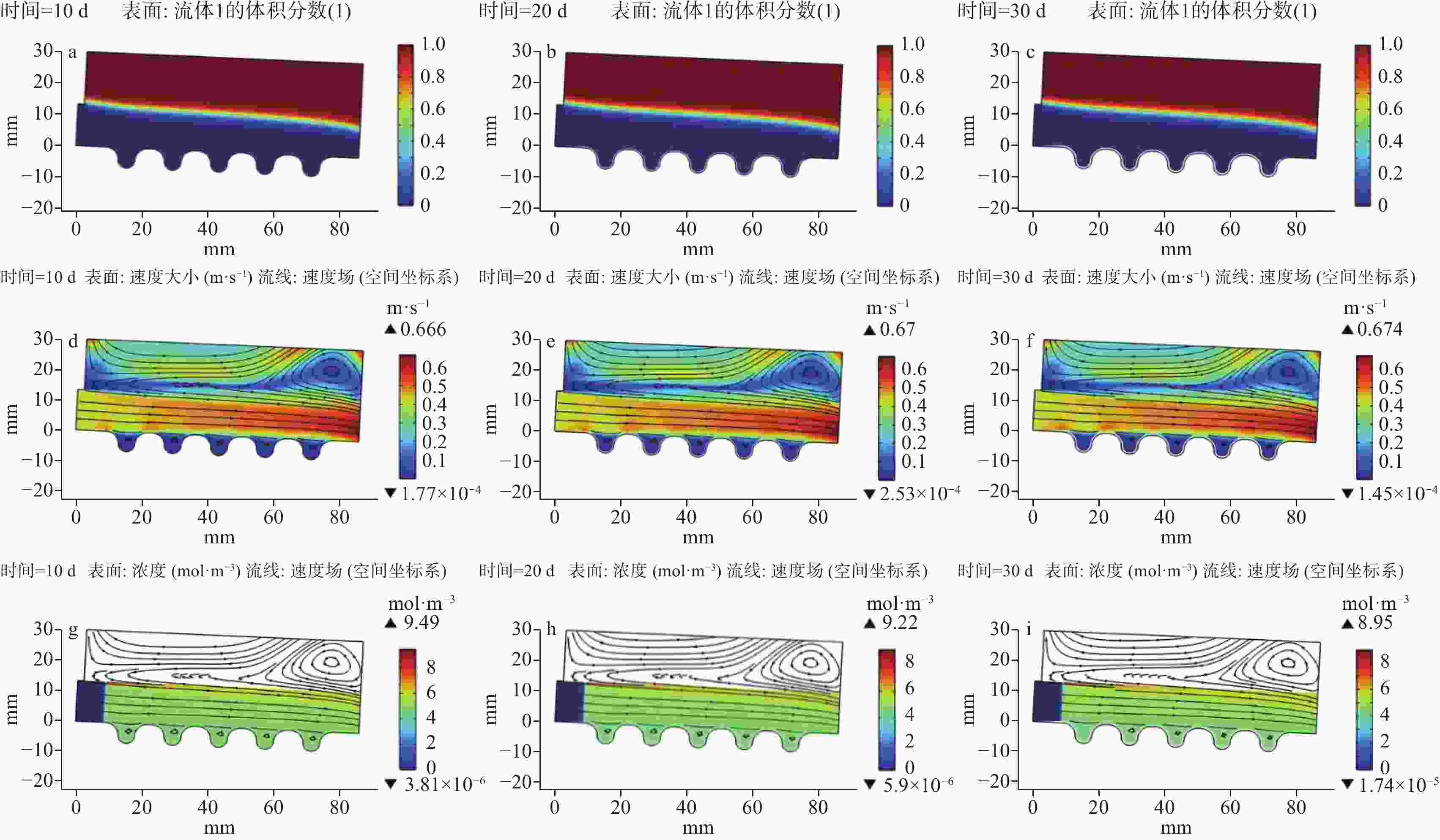
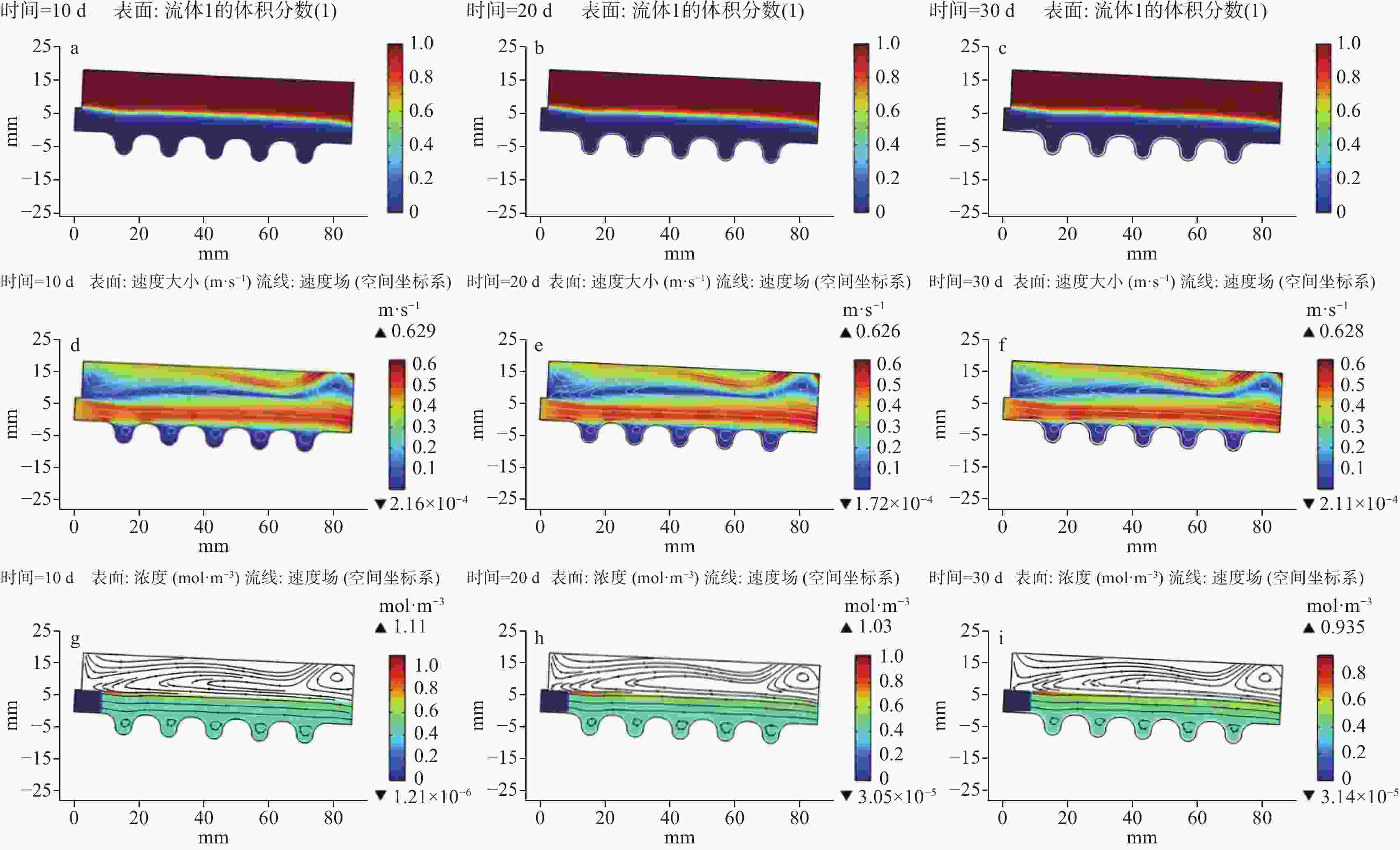
The frequent clogging of drainage pipes of tunnel engineering in the limestone regions has significantly impacted the long-term operation and maintenance of tunnels. To better solve this problem, in this study, a multi-field coupled numerical model was constructed to thoroughly analyze the formation mechanisms and key influencing factors of drainage pipe clogging. In recent days, fluid simulation has become an important tool for solving such problems, thanks to the rapid development of computational power. At present, numerous simulation models have been developed to simulate pipeline scaling; however, the conditions they simulate are often far cry from the actual working conditions of tunnel drainage pipes. To be specific, most simulations of pipeline scaling are conducted under full-pipe flow conditions, while the actual tunnel drainage pipes are rarely operated under full-pipe conditions. Considering this situation, this study integrated Fick’s law of mass transfer with the Navier-Stokes equations, thereby coupling fluid dynamics with chemical reaction kinetics through flow velocity. This coupling was achieved by incorporating mass transfer processes, which allowed for the determination of flow velocity and the distribution of calcium carbonate content within the pipe. Subsequently, a computational and simulation model was established for the curved boundaries of corrugated pipe by integrating an equation for calculating deposition thickness. To further enhance the model’s accuracy, a combination of the phase-field method and dynamic mesh technology was employed. The phase-field method simulated the movement of the gas-liquid interface, while dynamic mesh technology simulated flow channel contraction changes due to deposition. Moreover, changes in flow channel contraction may alter the flow velocity and the distribution of calcium carbonate content within the pipe, which in turn affected the contraction of the flow channel. Additionally, to ensure smooth mesh movement, mesh smoothing conditions were set, and functions were applied at the inlet and outlet to transition the movement rate from zero displacement to a specified velocity. In terms of boundary conditions, this model adopted a turbulence model. The inner wall friction coefficient of the pipe was calculated by formulas from hydraulic design manuals. Subsequently, the inner wall friction coefficient obtained from experiments was converted into an equivalent sand-grain roughness height using the Nikuradse formula, which was then used to represent various wall conditions in the model. Given that the model involves corrugated pipes, further adjustments to the Nikuradse formula are required. From the perspective of energy conservation, the energy loss caused by corrugated pipe grooves in water flow can be divided into two parts: firstly, the energy dissipation caused by imparting rotation to the stagnant water within the grooves; secondly, similar to a smooth pipe, energy loss caused by friction along the pipe wall. This portion of energy loss is related to the length of the wall. In this model, the equivalent length of the corrugated pipe is 1.2 times that of a smooth pipe with the same length. In condition of energy dissipation, and based on a series of trial calculations, the logarithmic function with base 10 was adjusted to a logarithmic function with base 11.3. The dynamic impact of crystal formation on flow field changes under free surface conditions was successfully simulated using this method. Simulation results indicate that the model developed in this study exhibits high predictive accuracy when the inner wall friction coefficient is within the range of 0.2 to 0.3, with an overall deviation between 10% and 20%. However, when the friction coefficient is below 0.2, significant deviations occur in the simulation results, which are higher than the actual deposition results. This may be due to the need for further optimization of the coefficients in the wall functions and deposition formulas under low-friction wall conditions. Moreover, when the friction coefficient exceeds 0.3, this model becomes inapplicable due to the failure of the boundary layer, which is caused by excessively high height of equivalent sand-grain roughness. In conclusion, based on the above research findings, this study has further applied the model to simulate the actual working conditions of drainage pipes in a tunnel in northern Guangdong. By predicting the clogging time and formulating corresponding treatment plans, this study provides scientific basis and technical support for the optimal design and clogging prevention of tunnel drainage systems. -
图 3 管内初期液体流动情况
a－g分别表现0~0.54s内某一时刻管内液体流动情况
Figure 3. Initial liquid flow conditions inside the pipe
图 4 工况1
a－c为10d、20d、30d水流动情况 d－f为10d、20d、30d流速云图 g－i为10d、20d、30d碳酸钙浓度分布图
Figure 4. Condition 1
图 5 工况2
a－c为10d、20d、30d水流动情况 d－f为10d、20d、30d流速云图 g－i为10d、20d、30d碳酸钙浓度分布图
Figure 5. Condition 2
图 6 工况3
a－c为10d、20d、30d水流动情况 d－f为10d、20d、30d流速云图 g－i为10d、20d、30d碳酸钙浓度分布图
Figure 6. Condition 3
图 7 工况4
a－c为10d、20d、30d水流动情况 d－f为10d、20d、30d流速云图 g－i为10d、20d、30d碳酸钙浓度分布图
Figure 7. Condition 4
图 8 工况5
a－c为10d、20d、30d水流动情况 d－f为10d、20d、30d流速云图 g－i为10d、20d、30d碳酸钙浓度分布图
Figure 8. Condition 5
图 9 工况6
a－c为10d、20d、30d水流动情况 d－f为10d、20d、30d流速云图 g－i为10d、20d、30d碳酸钙浓度分布图
Figure 9. Condition 6
图 11 实验结果与模拟结果对比图
11a-工况1的实验结果与模拟对比 11b-工况1的实验结果与模拟对比 11c-工况1的实验结果与模拟对比 11d- 工况1的实验结果与模拟对比 11e-工况1的实验结果与模拟对比 11f-工况1的实验结果与模拟对比
Figure 11. Comparison of experimental and simulation results
表 1 各个模拟工况数据
Table 1. Data for various simulation conditions
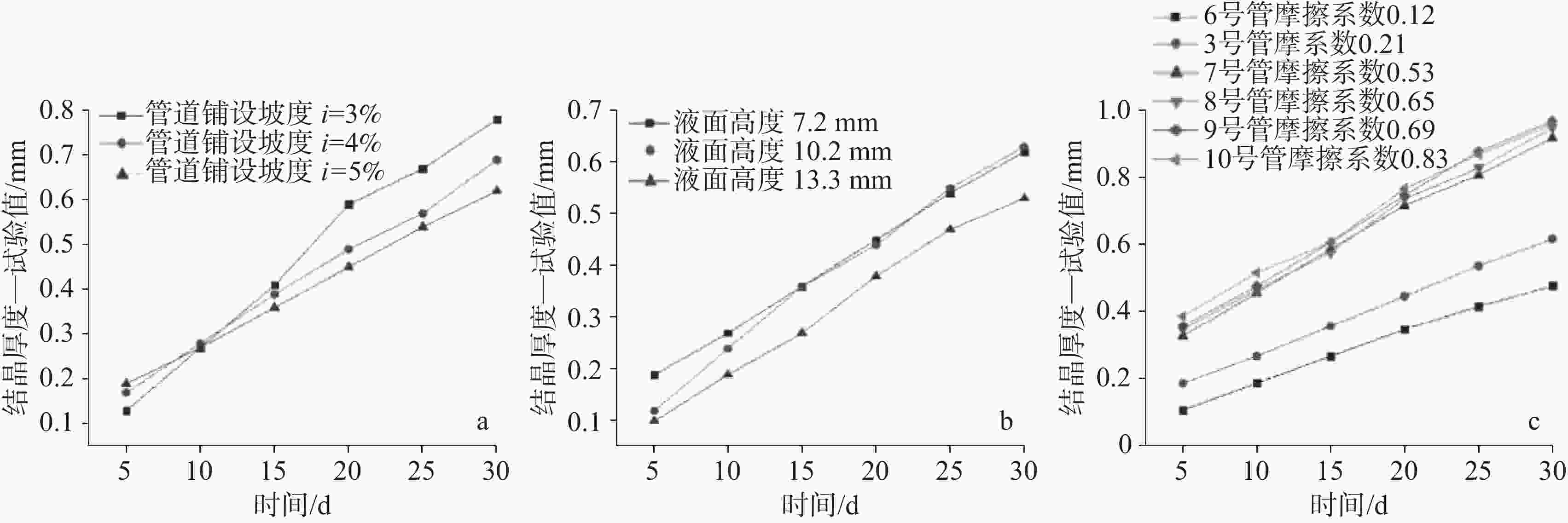
管道编号
（工况）液面高度/mm 管道坡度/% 初始流速/
cm·s−1内壁摩擦系数 1 7.1 3 41.36 0.26 2 6.9 4 43.73 0.21 3 7.2 5 41.28 0.23 4 10.2 5 41.83 0.27 5 13.3 5 39.86 0.24 6 6.9 5 43.36 0.12 7 7.1 5 42.11 0.53 8 6.8 5 40.41 0.65 9 7.0 5 43.78 0.69 10 7.3 5 39.19 0.83 
下载: 导出CSV
表 2 转换后数据
Table 2. Transformed data
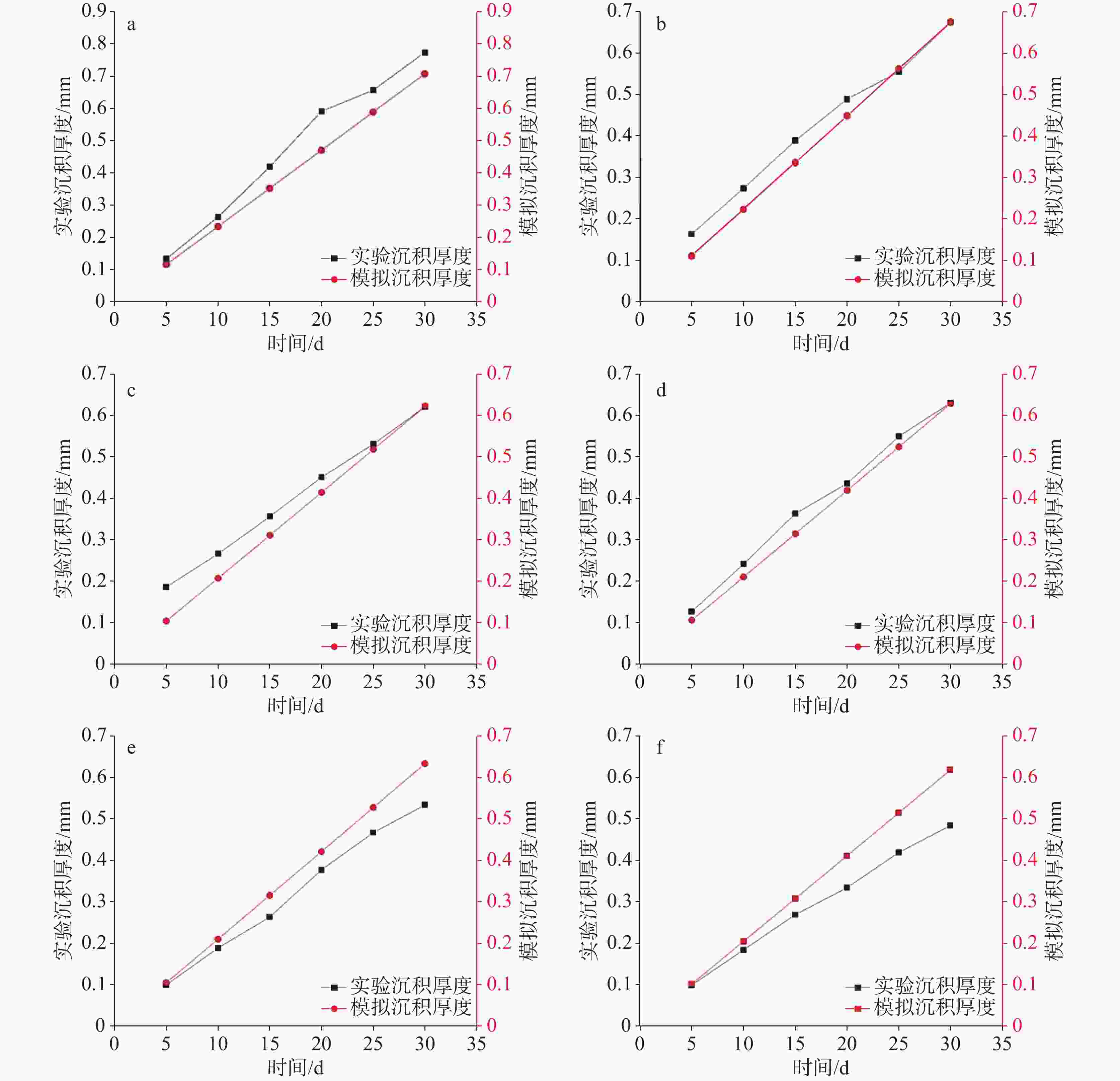
管道编号 内壁摩擦系数 等效砂砾粗糙高度/μm 1 0.26 3.78 2 0.21 2.89 3 0.23 3.25 4 0.27 2.71 5 0.24 3.43 6 0.12 1.23 7 0.53 7.70 8 0.65 9.05 9 0.69 9.46 10 0.83 10.76
下载: 导出CSV
表 3 平均沉积厚度对比
Table 3. Comparison of average sedimentary thickness
模拟工况 实验沉积厚度/
mm·d−1模拟沉积厚度/
mm·d−1相对误差/
%1 0.0260 0.0236 9.23 2 0.0230 0.0225 2.17 3 0.0207 0.0207 0 4 0.0210 0.0209 0.5 5 0.0177 0.0212 19.77 6 0.0160 0.0206 28.75
下载: 导出CSV
表 4 现场测试流速与离子浓度数据
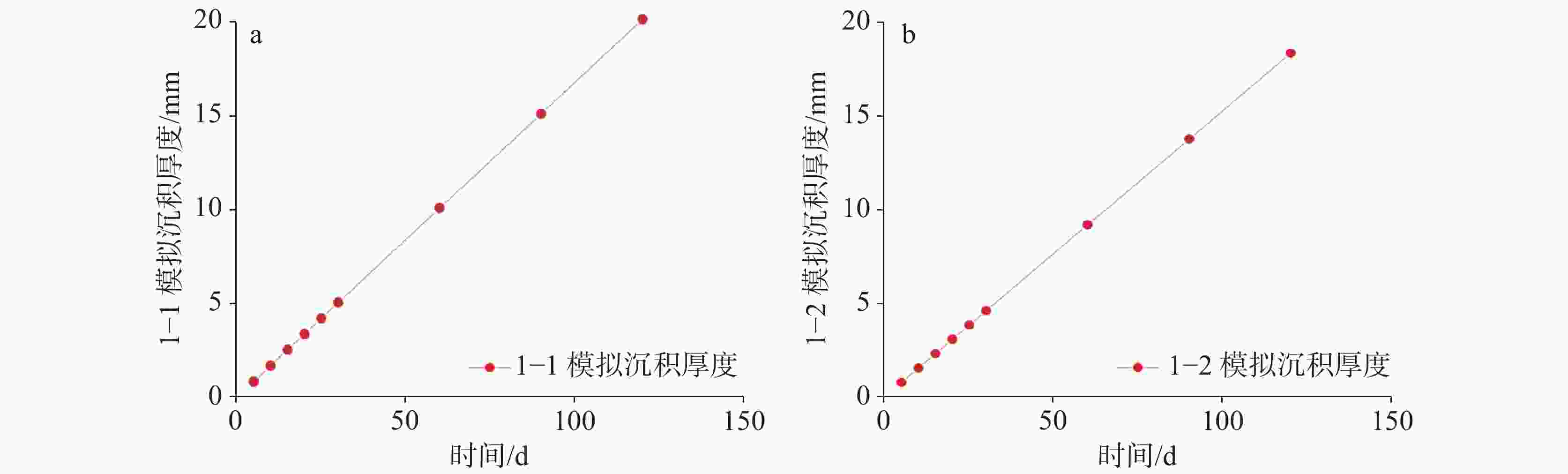
Table 4. On-site sampling data（On-site testing of flow rate and ion concentration data）
试样编号 钙离子浓度/mg·L−1 钠离子浓度/mg·L−1 镁离子浓度/mg·L−1 钡离子浓度/mg·L−1 流速/m·s−1 1-1 66.6316 1.0865 9.3366 0.1119 0.055 1-2 64.3725 0.7503 9.3031 0.1061 0.059
下载: 导出CSV
-
[1] 钱振宇, 彭海华, 吕建兵, 陈贡发. 华南地区灰岩隧道排水管化学结晶淤堵试验研究[J]. 现代隧道技术, 2021, 58(S1):143-9.QIAN Zhenyu, PENG Haihua, LV Jianbing, CHEN Gongfa. Experimental Study on Chemical Crystallization and Siltation in Drainage Pipe od Limestone Tunnels in South China[J]. Modern Tunnelling Technology, 2021, 58(S1): 143-149. [2] 卢冠楠, 王鹏, 杨蕴, 毛成君,吴咏敬,吴剑锋,董平,吴吉春. 岩溶区隧道排水系统地下水渗流结晶堵塞机理及阻垢技术研究综述[J]. 现代隧道技术, 2021, 58(6):11-20.LU Guannan, WANG Peng, YANG Yun, MAO Chengjun, WU Yongjing, WU Jianfeng, DONG Ping, WU Jichun. Review of Researches on Groundwater Seepage Induced Crystallization and Blockage Mechanism and Scale Inhibition Technology in the Tunnel Drainage System in Karst Areas[J]. Modern Tunnelling Technology, 2021, 58(6): 11-20. [3] CUI Yu Jun, Francisco Lamas-Lopez, Viet-Nam Trinh, Nicolas Calon, Sofia Costa D’Aguiar, Jean-Claude Dupla, Alain Robinet. Investigation of interlayer soil behaviour by field monitoring[J]. Transportation Geotechnics, 2014, 1(3): 91-105. doi: 10.1016/j.trgeo.2014.04.002 [4] JIA N, TASSIN B, CALON N, et al. Scaling in railway infrastructural drainage devices: site study[J]. Innovative Infrastructure Solutions, 2016, 1(1): 42. doi: 10.1007/s41062-016-0042-7 [5] WEDENIG M, EICHINGER S, BOCH R, et al. Understanding of tunnel drainage scale formation by in-situ monitoring[J]. Tunnelling and Underground Space Technology, 2023, 131: 104853. doi: 10.1016/j.tust.2022.104853 [6] WU Zilong, CUI Yujun, DENG Yongfeng. Role of surrounding soils and pore water in calcium carbonate precipitation in railway tunnel drainage system[J]. Transportation Geotechnics, 2019, 21: 100257. doi: 10.1016/j.trgeo.2019.100257 [7] 汤云涛, 周忠发, 汪炎林, 张结, 田衷珲, 薛冰清. 岩溶洞穴滴水CO2季节变化特征及来源分析:以大风洞为例[J]. 中国岩溶, 2021, 40(3):521-530.TANG Yuntao, ZHOU Zhongfa, WANG Yanlin, ZHANG Jie, TIAN Zhonghui, XUE Bingqing. Seasonal variations and sources of dripping CO_2, in karst caves: A case study of the Dafeng cave Guizhou Province[J]. Carsologica Sinica, 2021, 40(3): 521-530. [8] 缪仑, 周裕, 任辉. 非岩溶隧道排水系统结晶机理及防治措施研究[J]. 中国市政工程, 2022(5):66-69,124. doi: 10.3969/j.issn.1004-4655.2022.05.017MIAO Lun, ZHOU Yu, REN Hui. Study on Crystallization Mechanism & Prevention Measures of Non-Karst Tunnel Drainage System[J]. China Municipal Engineering, 2022(05): 66-69,124. doi: 10.3969/j.issn.1004-4655.2022.05.017 [9] 向坤, 周杰, 张学富, 黄超, 宋琳, 刘士洋. 碱性环境隧道排水管结晶规律室内试验研究[J]. 隧道建设(中英文), 2019, 39(S2):207-212.XIANG Kun, ZHOU Jie, ZHANG Xuefu, HUANG Chao, SU Lin, LIU Shiyang. Experimental Study on Crystallization Rule of Tunnel Drainpipe in Alkaline Environment[J]. Tunnel Construction, 2019, 39(S2): 207-212. [10] 聂崇欣, 饶军应, 刘建浩, 李元, 王石光, 谢财进. 隧道排水管道结晶体成分及结晶机理研究[J]. 河南理工大学学报(自然科学版), 2022, 41(6):196-202.NIE Chongxin RAO Junying LIU Jianhao LI Yuan, LI Yuan,WANG Shiguang,XIE Chaijin. Study on the crystal composition and mechanism of tunnel drainage system[J]. Journal of Henan Polytechnic University(Natural Science), 2022, 41(6): 196-202. [11] EICHINGER S, BOCH R, LEIS A, et al. Scale deposits in tunnel drainage systems − A study on fabrics and formation mechanisms[J]. Science of The Total Environment, 2020, 718: 137140. doi: 10.1016/j.scitotenv.2020.137140 [12] 董发勤, 陈禹衡, 代群威, 郑飞, 刘明学, 蒋忠诚, 张强, 李博文, Alper Baba, Mike O'Driscoll, Andelka Plenkovic-Moraj. 钙华体次生有机体系的界面结晶作用研究[J]. 中国岩溶, 2021, 40(1):34-43.DONG Faqin CHEN Yuheng DAl Qunwei ZHENG Fei, ZHENG Fei, LIU Mingxue, JIANG Zhongcheng, ZHANG Qiang, LI Bowen, Alper Baba, Mike O'Driscoll, Andelka Plenkovic-Moraj. Research progress on interfacial crystallization of travertine in secondary organic system[J]. Carsologica Sinica, 2021, 40(1): 34-43. [13] 董发勤, 郑飞, 代群威, 李琼芳, 陈禹衡, 刘明学, 蒋忠诚, 张强, 李博文, Alper BaBa, Andelka Plenkovic-Moraj. 钙华非经典沉积的纳米生长过程与调控机制初探:以九寨沟—黄龙钙华形成为例[J]. 中国岩溶, 2021, 40(1):55-67.DONG Faqin ZHENG Fei DAl Qunwei LI Qiongfang,LI Qiongfang, CHEN Yuheng, LIU Mingxue, JIANG Zhongcheng, ZHANG Qiang, LI Bowen, Alper BaBa, Andelka Plenkovic-Moraj. Research progress on interfacial crystallization of travertine in secondary organic system[J]. Carsologica Sinica, 2021, 40(1): 55-67. [14] WEI Liangwen, GUO Jingyi, ZHANG Xuefu, LI Yunqi, HUANG Peng. Study of Electric Field Impact on Crystallization in Tunnel Drainage Pipes in Hard Water Area[J]. Advances in Civil Engineering, 2021, 2021: 5584229. doi: 10.1155/2021/5584229 [15] 聂崇欣, 饶军应. 隧道排水系统结晶堵塞风险模糊评价模型研究[J]. 中国水运(下半月), 2021, 21(3):30-32.Nie Chongxin, Rao Junying. Research on Fuzzy Evaluation Model for Crystal Blockage Risk in Tunnel Drainage System[J]. China Water Transport, 2021, 21(3): 30-32. [16] Plummer L N,Wigley T M L ,Parkhurst D L. The kinetics of calcite dissolution in CO2-water systems at 5 degrees to 60 degrees C and 0.0 to 1.0 atm CO2[J]. American journal of science, 1978, 278(2): 179-216. doi: 10.2475/ajs.278.2.179 [17] Dreybrodt W,Buhmann D. A mass transfer model for dissolution and precipitation of calcite from solutions in turbulent motion[J]. Chemical Geology, 1991, 90(1-2): 107-122. doi: 10.1016/0009-2541(91)90037-R [18] 毛成君, 杨蕴, 吴剑锋, 董平, 吴吉春. 岩溶管道结晶堵塞水动力-化学反应耦合模拟对比研究[J]. 中国岩溶, 2023, 42(2):245-256.MAO Chengjun, YANG Yun, WU Jianfeng, DONG Ping, WU Jichun. Numerical simulation of crystal blockage in tunnel drainage pipe based ondynamic grid and level set[J]. Carsologica Sinica, 2023, 42(2): 245-256. [19] 周伟, 王永东, 李元飞, 王玲, 贾向波. 岩溶区隧道排水管道结晶沉淀水动力影响因素试验研究[J]. 公路, 2021, 66(3):347-352.ZHOU Wei, WANG Yongdong, LI Yuanfei, WANG Ling, JIA Xiangbo. Research on the lnfluence Factors of Crystallization and Sedimentation of Tunnel Drainage Pipeline in Karst Area[J]. Highway, 2021, 66(3): 347-352. [20] BRAHIM F, AUGUSTIN W, BOHNET M. Numerical simulation of the fouling process[J]. International Journal of Thermal Sciences, 2003, 42(3): 323-34. doi: 10.1016/S1290-0729(02)00021-2 [21] 王凯乐, 杨文奎, 史新成, 侯华,赵宇宏. 相场法研究AlxCuMnNiFe高熵合金富Cu相析出机理[J]. 物理学报, 2023, 72(7):319-333.WANG Kaile, YANG Wenkui, SHI Xincheng, HOU Hua, ZHAO Yuhong. Phase-field-method-studied mechanism of Cu-rich phase precipitation in AlxCuMnNiFe high-entropy alloy[J]. Acta Physica Sinica, 2023, 72(7): 319-333. [22] 姚雪蕾, 袁成清, 付宜风, 白秀琴. 管道内壁粗糙度对沿程阻力影响的FLUENT数值模拟分析[J]. 船海工程, 2015, 44(6):101-106,110. doi: 10.3963/j.issn.1671-7953.2015.06.024YAO Xuelei, YUAN Chengqing, FU Yifeng, BAI Xiuqin. Numerical Simulation of Effect of Wall Roughness on the On-way Resistance Based on FLUENT[J]. Ship & Ocean Engineering, 2015, 44(6): 101-106,110. doi: 10.3963/j.issn.1671-7953.2015.06.024 -
点击查看大图
图(13) / 表(4)
计量
- 文章访问数: 11
- HTML浏览量: 4
- PDF下载量: 2
- 被引次数: 0
