基于决策树模型的岩溶隧道涌水可能性快速判断

郭宝德; 张毅; 王新文; 陈志高; 董志明; 蒙彦

doi:10.11932/karst20240512

基于决策树模型的岩溶隧道涌水可能性快速判断——以桂河高速泗顶特长隧道为例

doi: 10.11932/karst20240512

郭宝德^1,,
张毅²,
王新文¹,
陈志高^3, ,,
董志明⁴,
蒙彦^5, ,

1.
华邦建投集团股份有限公司, 甘肃兰州 730199
2.
中铁二院工程集团有限责任公司, 四川成都 610031
3.
广西壮族自治区桂林水文工程地质勘察院有限公司，广西桂林 541002
4.
华杰工程咨询有限公司, 北京 100029
5.
自然资源部、广西岩溶动力学重点实验室/中国地质调查局岩溶塌陷防治技术创新中心/中国地质科学院岩溶地质研究所，广西桂林 541004

基金项目: 岩溶峰丛区特长公路隧道绿色建造关键技术研究（甘肃省建设科技项目/JK2024-39）；复杂岩溶管道流体力学过程与岩溶塌陷形成机制（国家基本科研业务重大项目）；岩溶塌陷地质灾害风险评价（DD20230441）

详细信息

作者简介:
郭宝德（1983－），男，硕士，工程师，现从事市政工程、公路工程施工、设计及科研管理等工作。E-mail：81708717@qq.com

通讯作者:
陈志高（1981－），高级工程师，长期从事水工环地质，岩土工程，地质灾害治理工程勘查、设计、施工等工作，E-mail: 281804974@qq.com

蒙彦（1978－），男，博士，研究员，博士生导师，研究方向为岩溶工程安全与地质灾害风险防控，E-mail: 54589998@qq.com。

中图分类号: U453.61；P642.25
计量
- 文章访问数: 40
- HTML浏览量: 8
- PDF下载量: 6
- 被引次数: 0
出版历程
- 收稿日期: 2023-08-01
- 录用日期: 2024-05-13
- 修回日期: 2024-02-27
- 网络出版日期: 2024-12-30
- 刊出日期: 2024-10-25

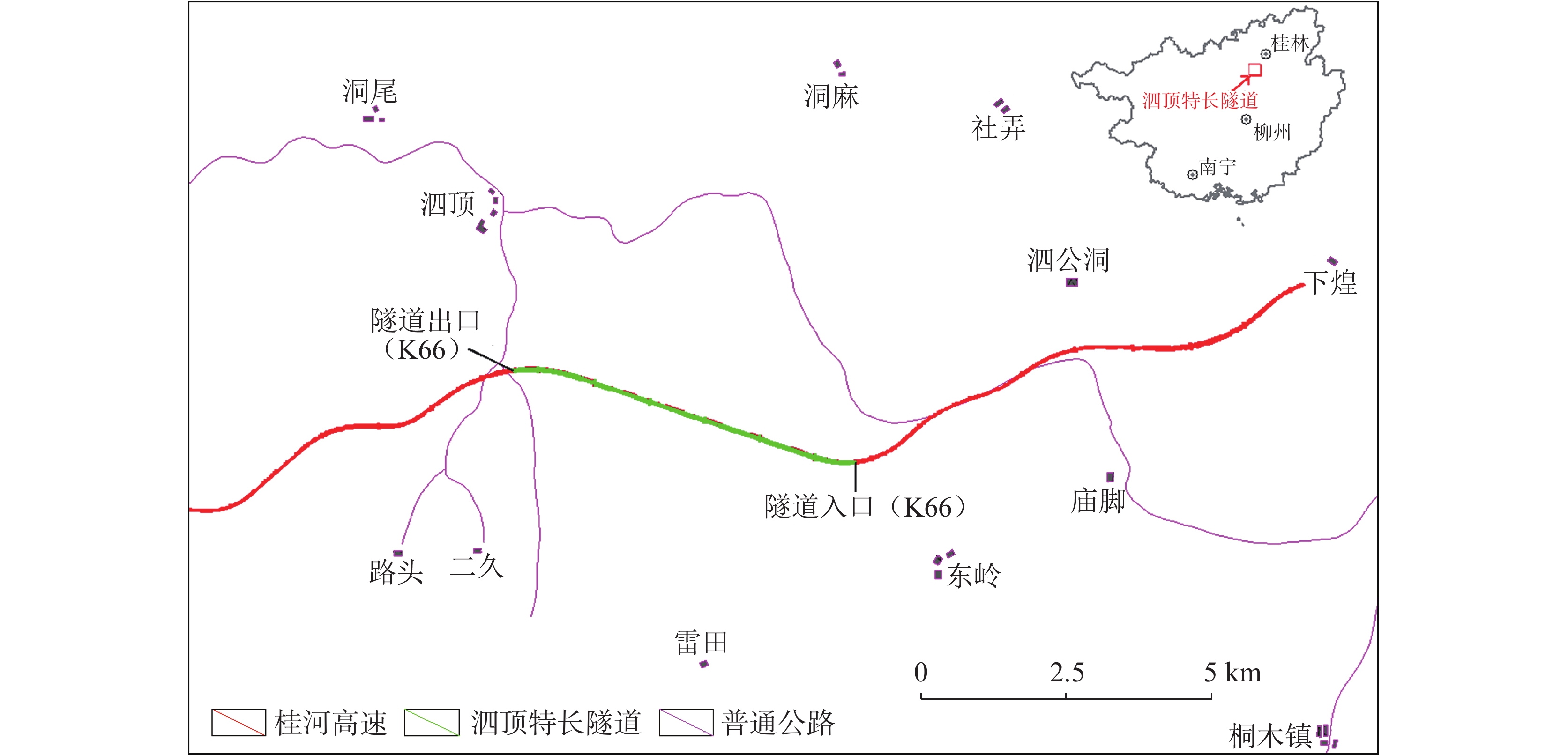
Rapid assessment of water and mud inrush likelihood in karst tunnels based on decision tree model: A case in Siding tunnel of Guihe expressway

GUO Baode^1
,,
ZHANG Yi²,
WANG Xinwen¹,
CHEN Zhigao^{3
, ,},
DONG Zhiming⁴,
MENG Yan^{5
, ,}

1.
Huabang Construction Investment Group Co., LTD, Lanzhou, Gansu 730199, China
2.
China Railway Eryuan Engineering Group Co., Ltd., Chengdu, Sichuan 610031, China
3.
Guilin Hydrological Engineering Geological Survey Institute Co., Ltd. of Guangxi Zhuang Autonomous Region, Guilin, Guangxi 541002, China
4.
CHELBI Engineering Consultants Incorporation, Beijing 100029, China
5.
Key Laboratory of Karst Dynamics, MNR & GZAR/Innovation Center of Karst Collapse Prevention, CGS/Institute of Karst Geology, CAGS, Guilin, Guangxi 541004, China

摘要

摘要: 涌水突泥是岩溶区隧道建设面临的重大地质安全问题，常造成严重的经济损失和人员伤亡。在实际工作中，对隧道涌水的可能性判断是决定是否采取相应预防和处置措施的重要依据。由于隧道涌水的地质影响因素错综复杂，这项工作以往多凭借经验进行定性分析，误报漏报率非常高，如何通过定量分析提高判断准确性亟待解决。作为一种探索，文章以桂河高速泗顶特长隧道为例，在水文地质调查分析研究的基础上，构建了基于决策树模型的岩溶隧道涌水突泥可能性快速判断方法、指标参数和预测模型。结果表明，泗顶特长隧道各里程段涌水概率最高为88.1%，发生大型涌水突泥的可能性非常大，实际建设过程中也正是在预测概率最高段发生了涌水突泥。该方法可以为后期类似工程有针对性地开展超前预报提供借鉴。
- 泗顶特长隧道 /
- 岩溶 /
- 决策树 /
- 隧道超前预报 /
- 概率 /
- 涌水突泥
Abstract: With the ongoing advancement of infrastructure projects, such as highways and railways, in China, karst tunnel construction is increasingly evolving towards longer, larger, and deeper dimensions. The problem of water and mud inrush in tunnels is becoming more and more severe. Effective measures for the advance prediction of water and mud inrush in tunnels have consistently been a pressing convern for management departments and engineering construction units. This issue also remains a significant challenge in related research fields. It is essential for us to assess the likelihood of tunnel water and mud inrush when determining whether to carry out advance prediction and identifying the appropriate mileage segment for conducting the prediction. This assessment is vital for targeted interventions, minimizing construction costs, and enhancing prediction accuracy. To some extent, the assessment of the likelihood of water inrush in tunnels falls under the category of advance prediction and serves as the foundational element for conducting such prediction.The rapid assessment of the likelihood of water inrush in karst tunnels is an important basis for deciding whether to carry out advance prediction and to take measures for emergency treatment. This rapid assessment was often absent in previous work. Even though assessments for the likelihood of water inrush were conducted occasionally in several tunnels, they were primarily based on qualitative methods of geological analysis. This often resulted in discrepancies from actual conditions, leading to misjudgments. In some tunnels, significant manpower and resources were sometimes expended on predicting water inrush, advance prediction, and tunnel waterproofing design, yet no water inrush occurred. Conversely, the sections of some tunnels that were neither predicted nor adequately protected experienced severe water and mud inrush. Therefore, the accuracy of assessments regarding the likelihood of water inrush in tunnels is crucial for determining whether to undertake subsequent prediction and prevention efforts. This study explored Siding tunnel on Guihe expressway as a case study. Utilizing karst hydrogeological surveys and research, in conjunction with geophysical exploration and drilling data, the study started with the degree of karst development and the relationship between the tunnel and karst groundwater, both of which are closely associated with water and mud inrush in the tunnel. Ten representative parameters for the decision tree model were identified and quantified, including karst rates in the transverse and longitudinal sections of the tunnel, as well as the vertical zonation relationship between the tunnel and groundwater. Based on this analysis, a rapid assessment method, along with indicator parameters and a predictive model for assessing the likelihood of water and mud inrush in the karst tunnel, was developed and practically validated. The results indicate that the highest probability of water inrush in each mileage of Siding tunnel is 88.1%, suggesting a very high probability of large-scale water and mud inrush. Notably, during the actual construction process, the occurrence of water and mud inrush was observed in the segment with the highest predicted likelihood.Using a decision tree model to analyze and assess the likelihood of water and mud inrush in the tunnel represents a valuable exploratory study. The decision tree model offers the advantage of selecting the optimal solution among multiple complex options, effectively mitigating errors arising from human experience-based judgments. This approach enhances the scientific rigor geological analysis related to assessments of water and mud inrush in tunnels. According to the principles of the decision tree method, this model can quickly assess both the likelihood and magnitude of water inrush based on various critical values for water inrush sizes and the probabilities associated with different branches. Furthermore, it can determine the probability of a specific scale of water inrush based on the rapid assessment of the likelihood of water inrush. In the future, it will be essential to refine the indicator parameters of scheme branches, state branches, and probability branches on different scenarios of water and mud inrush in tunnels. This refinement will provide targeted guidance for advance predictions in similar projects.
- Siding tunnel /
- karst /
- decision tree /
- tunnel advance prediction /
- probability /
- water and mud inrush

HTML

图 1 泗顶隧道交通位置图

Figure 1. Location of Siding tunnel

下载: 全尺寸图片幻灯片

图 2 泗顶隧道岩溶水文地质简图

Figure 2. Diagram of karst hydrogeology of Siding tunnel

下载: 全尺寸图片幻灯片

图 3 岩溶地下水水位与隧道交割关系图

Figure 3. Relationship between tunnel and karst groundwater level

下载: 全尺寸图片幻灯片

图 4 隧道涌水突泥决策树模型

Figure 4. Decision tree model of water and mud inrush in the tunnel

下载: 全尺寸图片幻灯片

图 5 泗顶特长隧道涌水可能性决策树模型计算结果（K66）

Figure 5. Calculation results of decision tree model for the likelihood of water inrush in Siding tunnel (K66)

下载: 全尺寸图片幻灯片

图 6 泗顶特长隧道实际涌水位置（K66+660）

Figure 6. Location of water inrush in Siding tunnel (K66+660)

下载: 全尺寸图片幻灯片

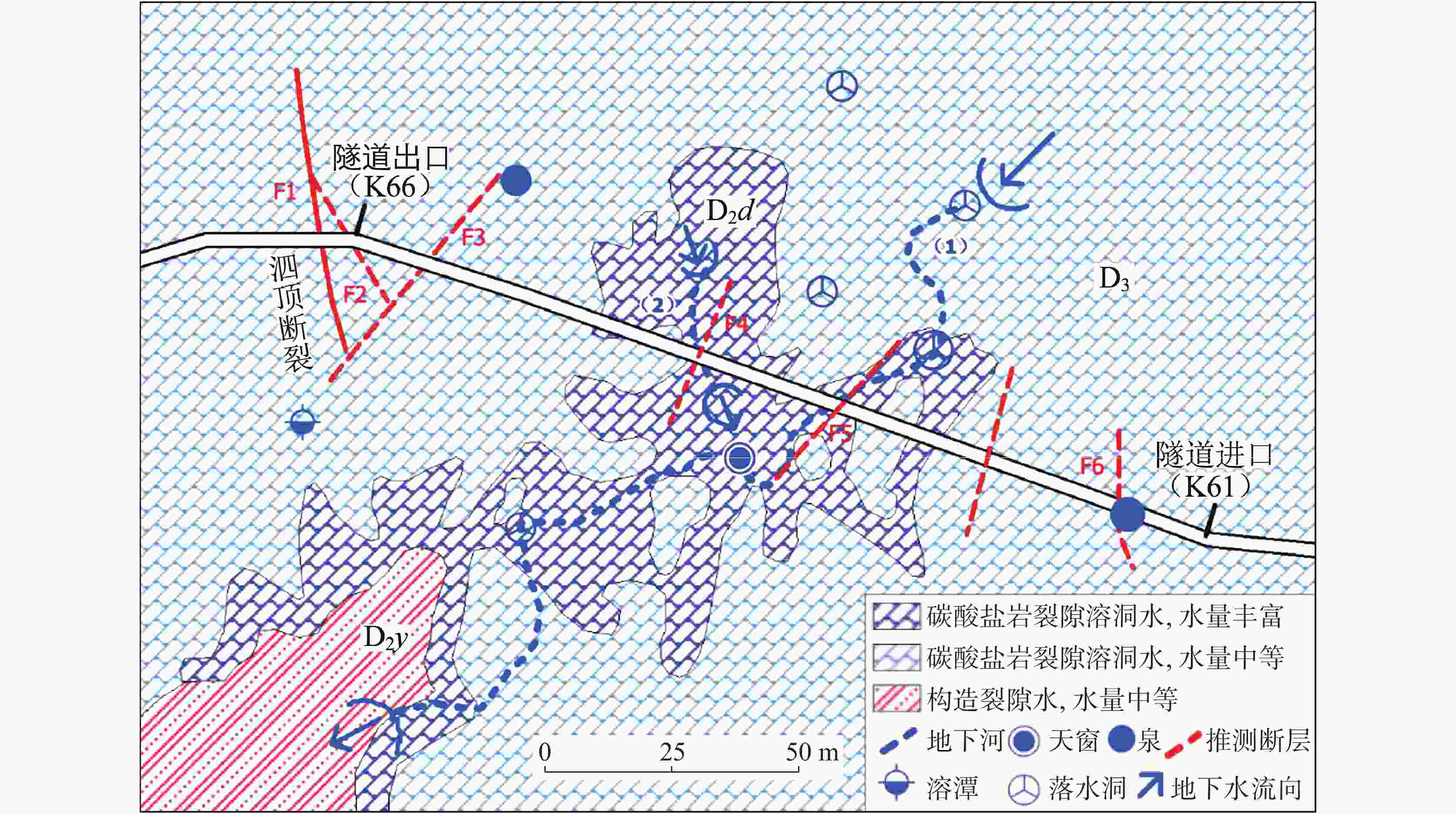
表 1 隧道各里程岩溶发育数量及规模

Table 1. Number and scale of karst developed in each mileage of the tunnel

里程	地表岩溶数量 /处	岩性分界线条数/处	地质构造交割条数/处	钻孔遇洞率/%	纵断面岩溶规模超过3 m数量 /处及占比/%		纵断面岩溶规模1~3 m数量 /处及占比/%		纵断面岩溶规模小于1 m数量 /处及占比/%		隧道轴线岩溶率/%	横断面最大岩溶率/%
k61+000~k62+000	11	1	1	24.39	2	18.18	9	2.15	81.82	0	35.45	0
k62+000~k63+000	7	0	0	19.73	0	0	5	4.33	71.43	2	24.29	28.57
k63+000~k64+000	0	0	2	0	0	0	0	0	0	0	0	0
k64+000~k65+000	3	0	1	11.53	1	33.33	2	8.14	66.67	0	26.67	0
k65+000~k66+000	7	0	0	20.31	2	28.57	3	5.12	42.86	2	32.86	28.57
k66+000~k67+000	9	1	3	26.36	3	33.33	5	12.87	55.56	1	37.78	11.11
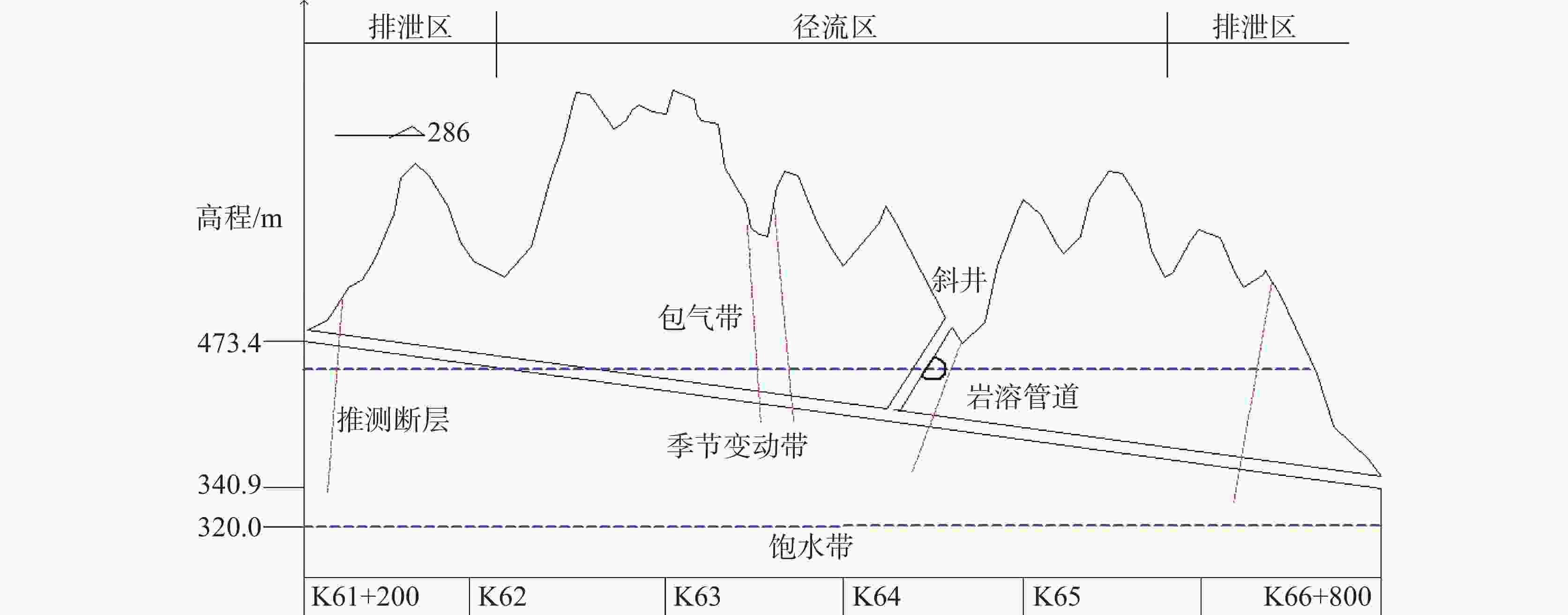
注：本表中的岩溶规模是指纵断面揭露的溶洞直径，溶槽、缝隙宽度。 Note: The karst scale in this table refers to the diameter of the karst cave, the width of the solution trough and the gap exposed by the longitudinal section.

下载: 导出CSV

表 2 隧道各里程岩溶地下水与隧道关系

Table 2. Relationship between tunnel and karst groundwater in each mileage of the tunnel

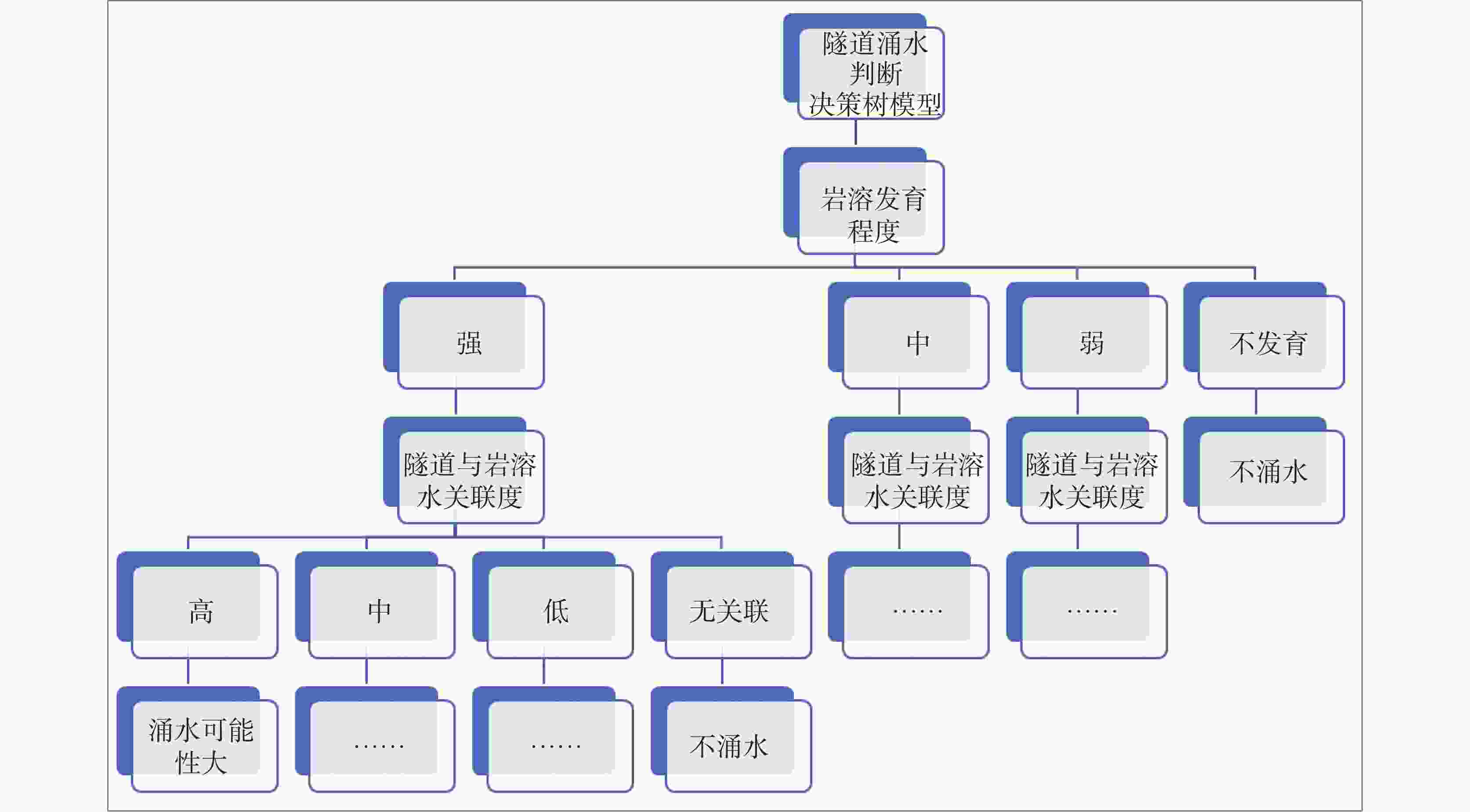
里程	是否排泄区（是1，否0）	是否径流区（是1，否0）	枯水位与隧洞最小距离/m（负为水面下）	是否存在强径流带（地下河）（是1，否0）
k61+000~k62+000	1	0	13.4	0
k62+000~k63+000	0	1	0	0
k63+000~k64+000	0	1	−11.84	0
k64+000~k65+000	0	1	−35.51	1
k65+000~k66+000	0	1	−59.18	0
k66+000~k67+000	1	0	−78.11	1

下载: 导出CSV

表 3 隧道涌水突泥快速判别决策树模型物理参数表

Table 3. Physical parameters of decision tree model for rapid assessment of water and mud inrush in the tunnel

决策	方案枝	状态枝	概率枝	概率条件	可能性
1涌水 2不涌水	1)可能性极大（加权概率>90%） 2)可能性大（60%<加权概率≤90%） 3)可能性中等（30%≤加权概率≤60%） 4) 可能性小（10%≤加权概率<30%） 5）可能性极小（加权概率<10%）	(1)岩溶发育程度	①地表岩溶点密度	>10个·km⁻¹	大
				2~10个·km⁻¹	中
				<2个·km⁻¹	小
			②岩性分界线密度	密度>2条·km⁻¹	大
				1<密度≤2条·km⁻¹	中
				密度≤1条·km⁻¹	小
			③断层线密度	密度>2条·km⁻¹	大
				1<密度≤2条·km⁻¹	中
				密度≤1条·km⁻¹	小
			④钻孔遇溶率	遇洞率≥30%	大
				10%≤遇洞率<30%	中
				遇洞率<10%	小
			⑤隧道纵断面溶洞直径、缝隙宽度	单段连续规模≥3 m的占比≥30%，或者单段连续规模≥3 m的占比<30%，并且1 m≤单段连续规模<3 m 的占比≥60%	大
				其他情况	中
				单段连续规模<1 m的占比<10%，并且其他规模不发育	小
			⑥隧道轴线岩溶率	线岩溶率≥60%	大
				30%≤线岩溶率<60%	中
				线岩溶率<30%	小
			⑦隧道横断面（掌子面）最大岩溶率	面岩溶率>30%	大
				面岩溶率10%~30%	中
				面岩溶率<10%	小
		(2)隧道与岩溶水关联度	⑧补径排关系	排泄区	大
				径流区	中
				补给区	小
			⑨隧道与地下水位关系	隧道位于季节变动带下部	大
				隧道位于季节变动带中部	中
				隧道位于季节变动带上部及包气带	小
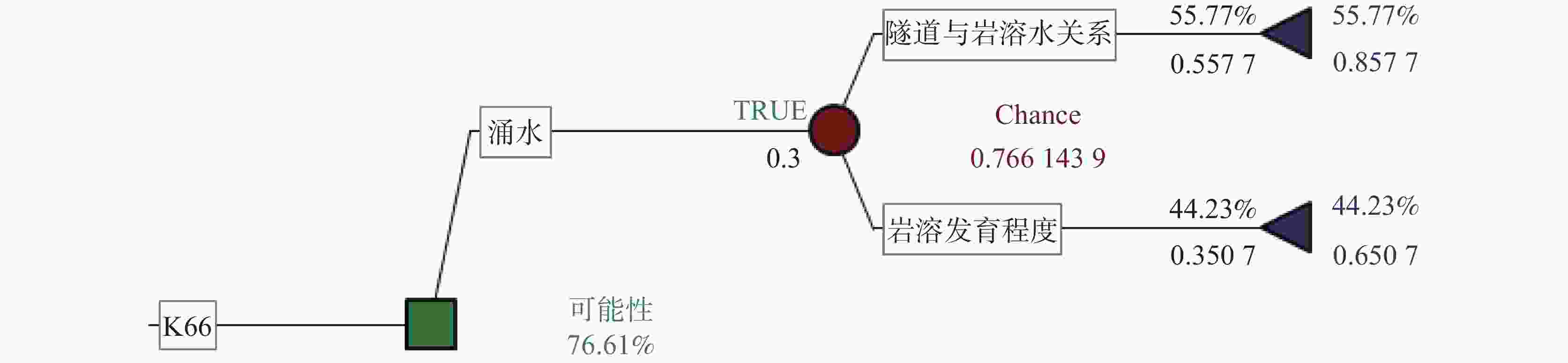
			⑩隧道穿越强径流带（地下河等）情况	密度≥1条·km⁻¹	大
				0<密度<1条·km⁻¹	中
				0条·km⁻¹	小

下载: 导出CSV

表 4 隧道涌水突泥快速判别决策树模型计算参数表（K66）

Table 4. Calculation parameters of decision tree model for rapid assessment of water and mud inrush in the tunnel (K66)

里程段	状态枝	概率条件	涌水权重/%	对应可能性	可能性加权/%	加权涌水权重/%	状态枝概率/%
k66+000~k67+000	岩溶发育程度	地表岩溶点密度	1.65	中	75.00	1.24	33.61
		岩性分界线数量	3.56	小	25	0.89
		断层线密度	4.90	大	100	4.90
		钻孔遇洞率	2.93	小	25	0.73
		纵断面岩溶规模	9.82	大	100	9.82
		轴线岩溶率	8.15	中	75.00	6.11
		横断面岩溶率	13.22	中	75.00	9.92
	隧道与岩溶水关联度	补径排关系	1.03	大	100	1.03	55.77
		地下水位	20.45	大	100	20.45
		强径流带数量	34.29	大	100.00	34.29

下载: 导出CSV

表 5 隧道不同里程段状态枝概率

Table 5. Probability of state branch in each mileage of the tunnel

里程段	状态枝	状态枝概率/%
k61+000~k62+000	岩溶发育程度	25.20
k61+000~k62+000	隧道与岩溶水关联度	14.72
k62+000~k63+000	岩溶发育程度	24.87
k62+000~k63+000	隧道与岩溶水关联度	14.46
k63+000~k64+000	岩溶发育程度	13.51
k63+000~k64+000	隧道与岩溶水关联度	13.94
k64+000~k65+000	岩溶发育程度	20.71
k64+000~k65+000	隧道与岩溶水关联度	50.40
k65+000~k66+000	岩溶发育程度	24.87
k65+000~k66+000	隧道与岩溶水关联度	29.80
k66+000~k67+000	岩溶发育程度	35.07
k66+000~k67+000	隧道与岩溶水关联度	55.77

下载: 导出CSV

参考文献(13)

[1]	蒋树屏, 林志, 王少飞. 2018年中国公路隧道发展[J]. 隧道建设, 2019, 39(7):1217-1220. JIANG Shuping, LIN Zhi, WANG Shaofei. Development of highway tunnels in China in 2018[J]. Tunnel Construction, 2019, 39(7): 1217-1220.
[2]	李术才, 王康, 李利平, 周宗青, 石少帅, 柳尚. 岩溶隧道突水灾害形成机理及发展趋势[J]. 力学学报, 2017, 49(1):22-30. doi: 10.6052/0459-1879-16-345 LI Shucai, WANG Kang, LI Liping, ZHOU Zongqing, SHI Shaoshuai, LIU Shang. Mechanical mechanism and development trend of water-inrush disasters in karst tunnels[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(1): 22-30. doi: 10.6052/0459-1879-16-345
[3]	蒙彦, 雷明堂. 岩溶区隧道涌水研究现状及建议[J]. 中国岩溶, 2003, 22(4):287-292. doi: 10.3969/j.issn.1001-4810.2003.04.007 MENG Yan, LEI Mingtang. The advance and suggestion for the study on discharge rate in karst tunnel gushing[J]. Carsologica Sinica, 2003, 22(4): 287-292. doi: 10.3969/j.issn.1001-4810.2003.04.007
[4]	Thomas Goetz. The decision tree[M]. Rodale, 2010 (ISBN10: 9781605297293).
[5]	伍小刚. 隧道超前地质预报物探方法选择与解译阈值研究[D]. 成都:成都理工大学, 2020. WU Xiaogang. Study on method selection and interpretation threshold of advanced geological forecast in tunnel[D]. Chengdu: Chengdu University of Technology, 2020.
[6]	韩行瑞. 岩溶隧道涌水及其专家评判系统[J]. 中国岩溶, 2004, 23(3):213-218. HAN Xingrui. Karst water bursting in tunnel and expert judging system[J]. Carsologica Sinica, 2004, 23(3): 213-218.
[7]	林永生, 邹胜章, 朱丹尼. 岩溶隧道涌水原因揭秘[J]. 中国矿业, 2020, 29(Suppl.1):582-583, 586. LIN Yongsheng, ZOU Shengzhang, ZHU Danni. The causes of water bursting in karst tunnel[J]. China Mining Magazine, 2020, 29(Suppl.1): 582-583, 586.
[8]	王健华, 李术才, 李利平, 许振浩. 隧道岩溶管道型突涌水动态演化特征及涌水量综合预测[J]. 岩土工程学报, 2018, 40(10):1880-1888. doi: 10.11779/CJGE201810015 WANG Jianhua, LI Shucai, LI Liping, XU Zhenhao. Dynamic evolution characteristics and prediction of water inflow of karst piping-type water inrush of tunnels[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(10): 1880-1888. doi: 10.11779/CJGE201810015
[9]	杨光. 基于多源异构数据的滑坡灾害决策树预测模型研究[D]. 北京:中国地质大学(北京), 2016. YANG Guang. Research on decision-tree prediction model of landslide based on multi-source heterogeneous data[D]. Beijing: China University of Geosciences (Beijing), 2016.
[10]	洪郡伶. 整合层次分析法及决策树於设备投资决策之实证研究[D]. 北京:清华大学, 2017. HONG Junling. An empirical investigation of decision making on investment of equipment using analytic hierarchy process and decision tree analysis[D]. Beijing: Tsinghua University, 2017.
[11]	陈语. 隧道大变形灾害动态风险评估与支护决策研究[D]. 成都:成都理工大学, 2017. CHEN Yu. Dynamic risk assessment and risk-based support decision analysis on tunnel squeezing[D]. Chengdu: Chengdu University of Technology, 2017.
[12]	丁胜祥, 董增川, 张莉. 基于决策树算法的洪水预报模型[J]. 水力发电, 2011, 37(7):8-11, 33. DING Shengxiang, DONG Zengchuan, ZHANG Li. Flood forecasting model based on decision tree algorithm[J]. Water Power, 2011, 37(7): 8-11, 33.
[13]	Yongli Gao, E Calvin Alexander Jr. Sinkhole hazard assessment in Minnesota using a decision tree model[J]. Environmental Geology, 2008, 54(5): 945-956. doi: 10.1007/s00254-007-0897-1