基于颗粒流的覆盖型岩溶地面塌陷动态演化特征研究

师海; 贾智磊; 白明洲; 张晔; 孙子冰

doi:10.11932/karst20240509

基于颗粒流的覆盖型岩溶地面塌陷动态演化特征研究

doi: 10.11932/karst20240509

师海^{1, 2,},
贾智磊^1,,
白明洲^{1, 3},
张晔¹,
孙子冰¹

1.
北京交通大学土木建筑工程学院, 北京 100044
2.
轨道工程北京市重点实验室, 北京 100044
3.
北京市轨道交通线路安全与防灾工程技术研究中心, 北京 100044

基金项目: 国家自然科学基金项目（41907260、42172311）；中央引导地方科技发展资金项目（216Z3802G)

详细信息

作者简介:
师海（1987－），男，博士，副教授，主要从事岩溶灾害防治和地面塌陷领域的教学科研工作。E-mail：shihai@bjtu.edu.cn

中图分类号: P642.5
计量
- 文章访问数: 37
- HTML浏览量: 11
- PDF下载量: 10
- 被引次数: 0
出版历程
- 收稿日期: 2022-10-07
- 录用日期: 2023-05-02
- 修回日期: 2023-03-30
- 网络出版日期: 2024-12-30
- 刊出日期: 2024-10-25

Dynamic evolution characteristics of ground collapse of covered karst based on particle flow

SHI Hai^{1, 2
,},
JIA Zhilei^1
,,
BAI Mingzhou^{1, 3},
ZHANG Ye¹,
SUN Zibing¹

1.
School of Civil Engineering, Beijing Jiaotong University, Beijing100044, China
2.
Beijing Key Laboratory of Track Engineering, Beijing 100044, China
3.
Beijing Engineering and Technology Research Center of Rail Transit Line Safety and Disaster Prevention, Beijing 100044, China

摘要

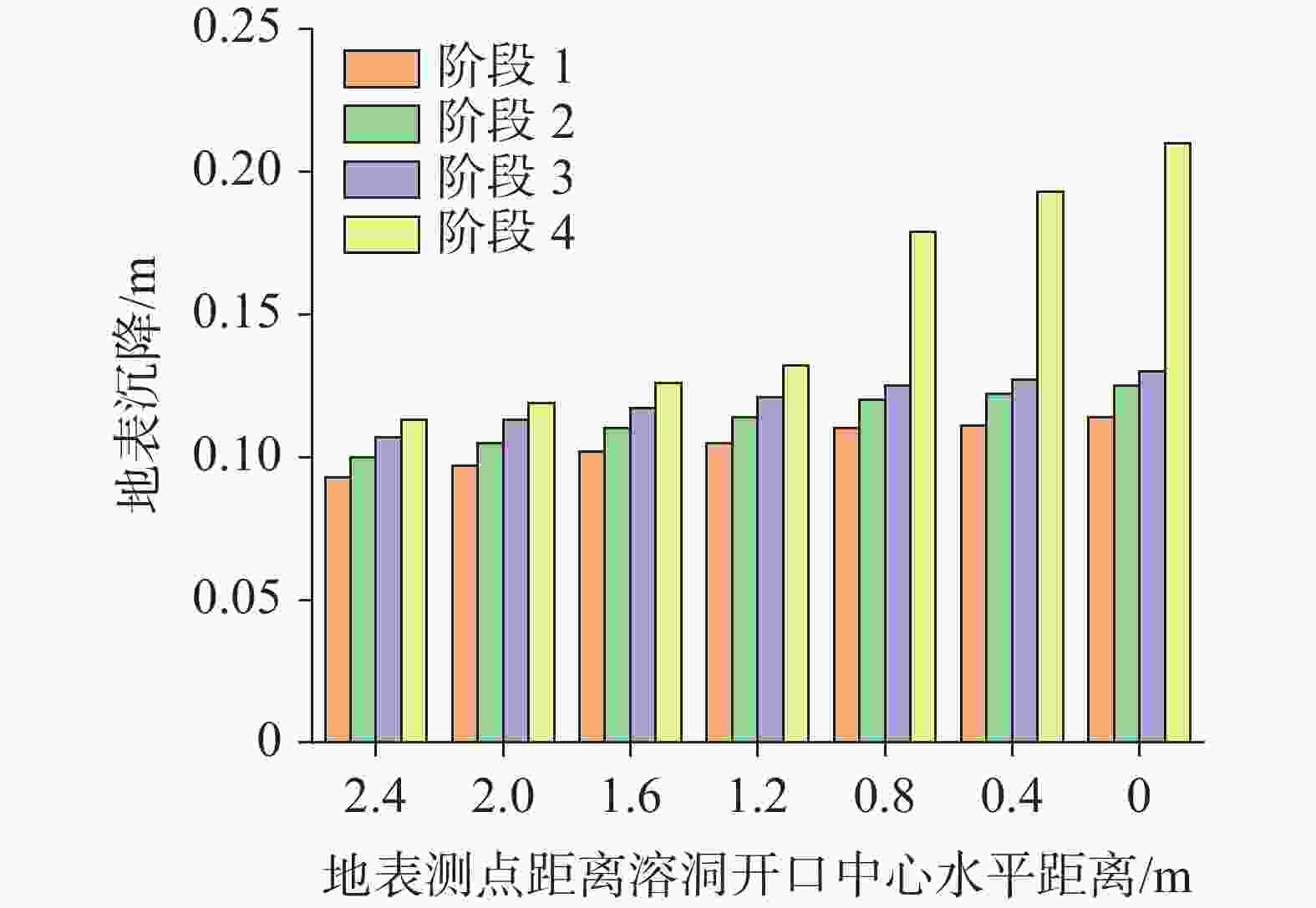
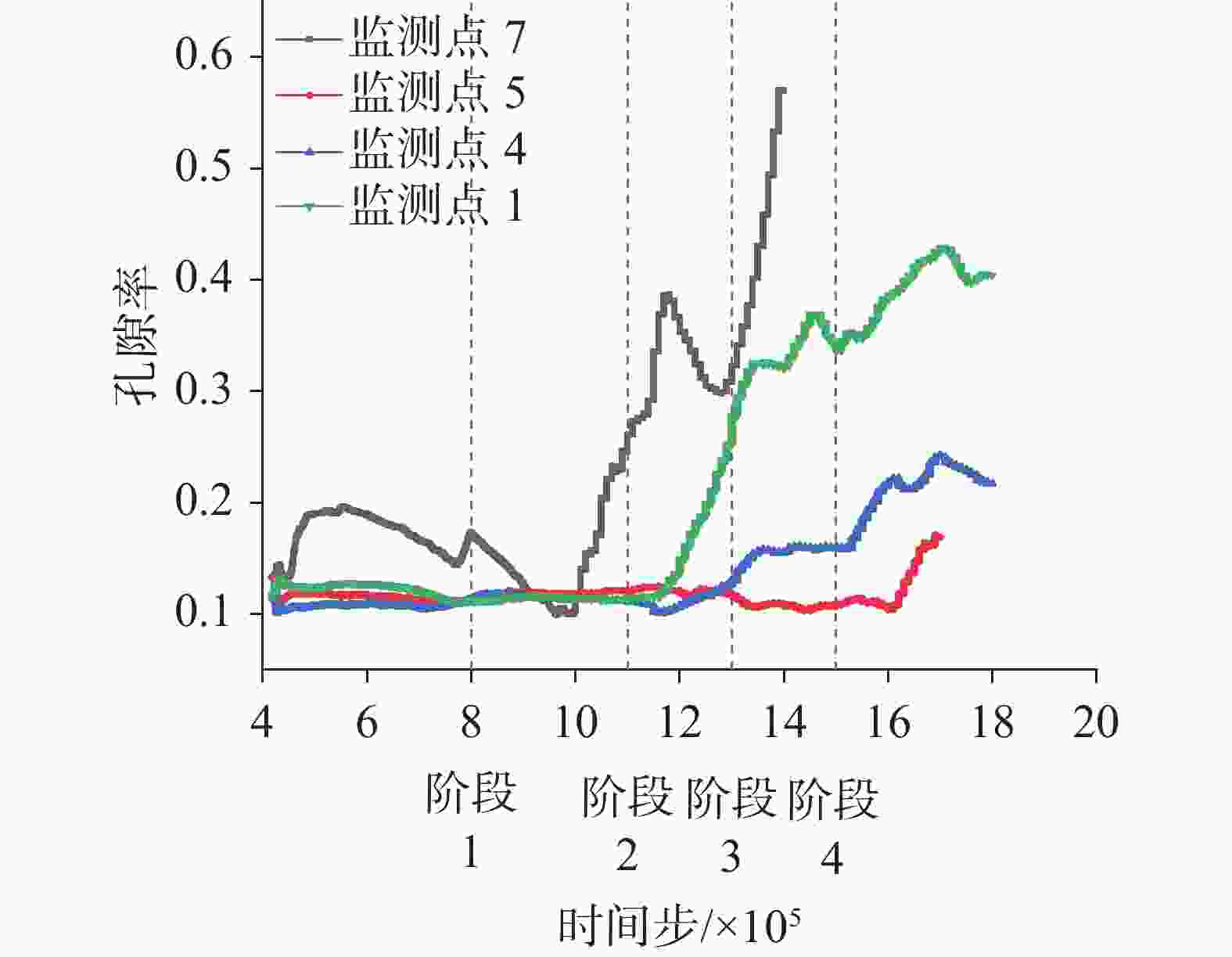
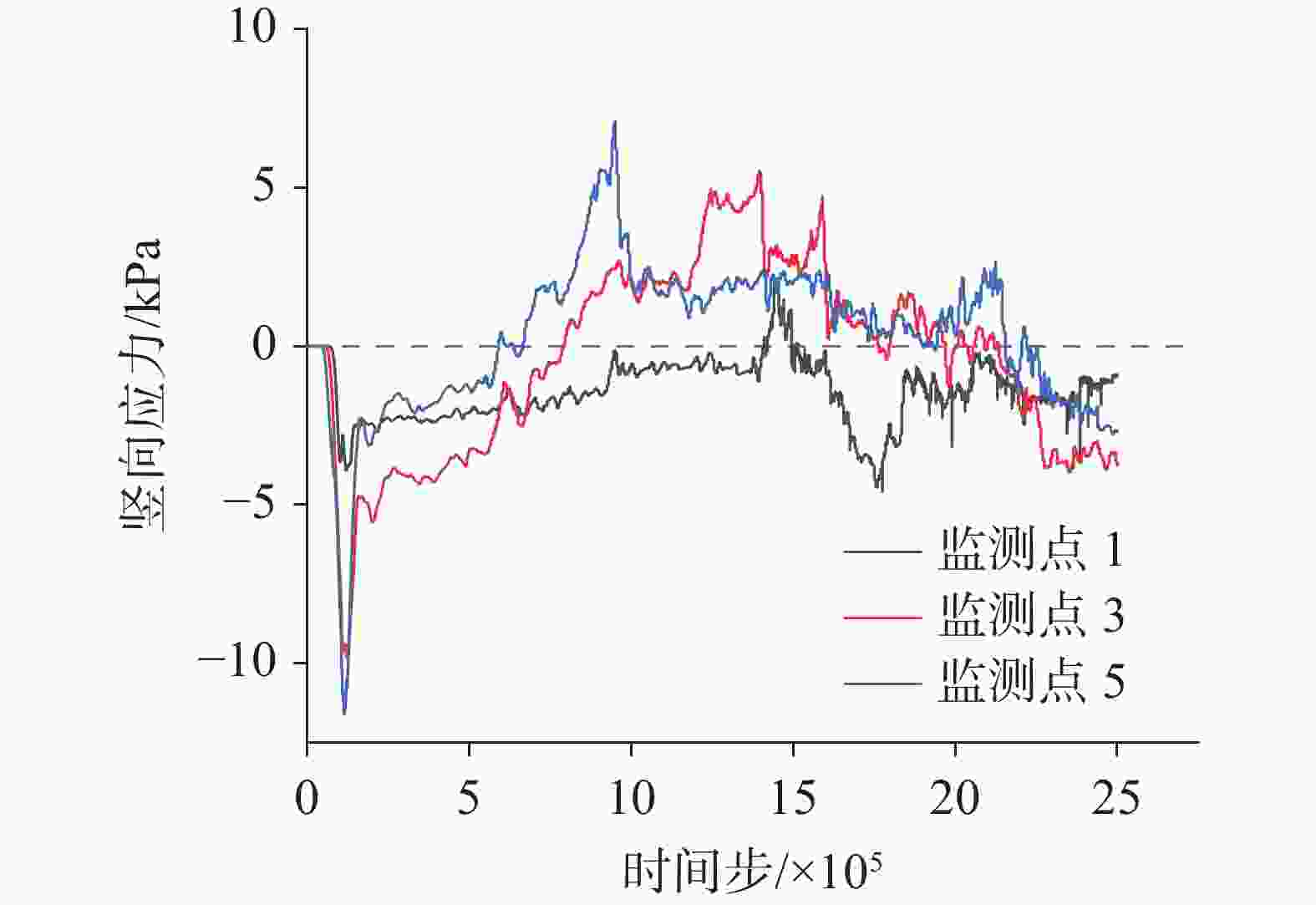
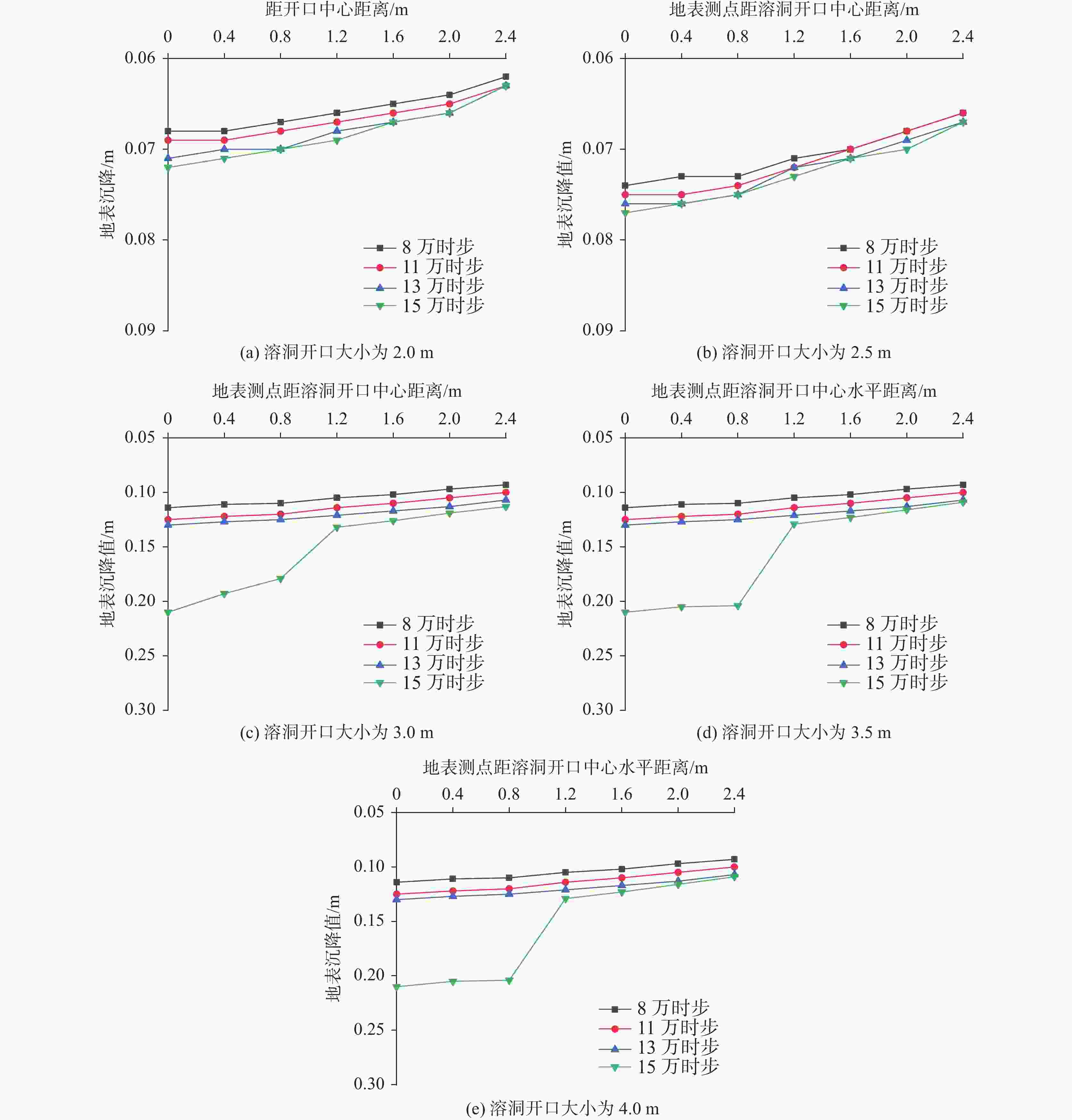
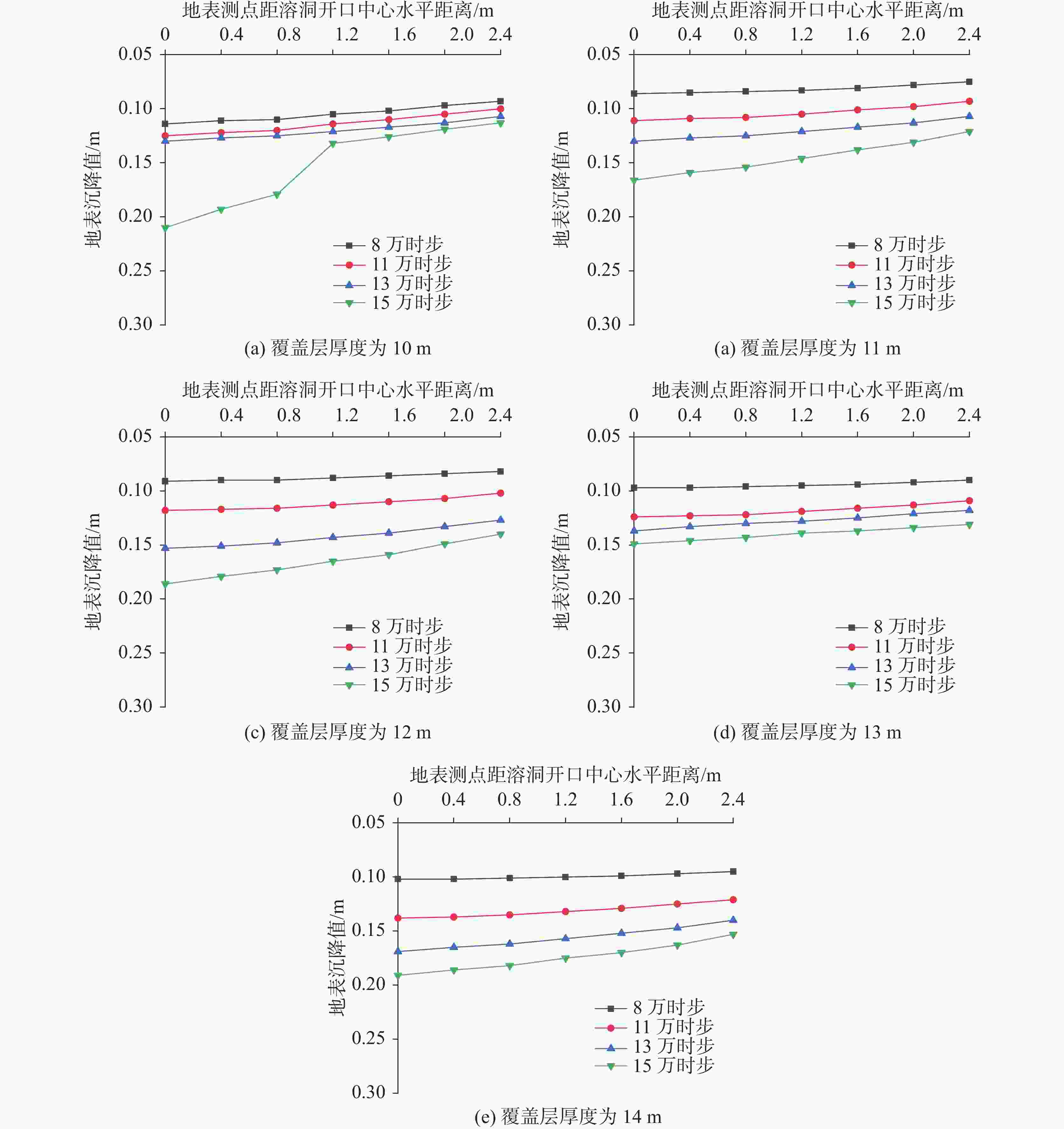
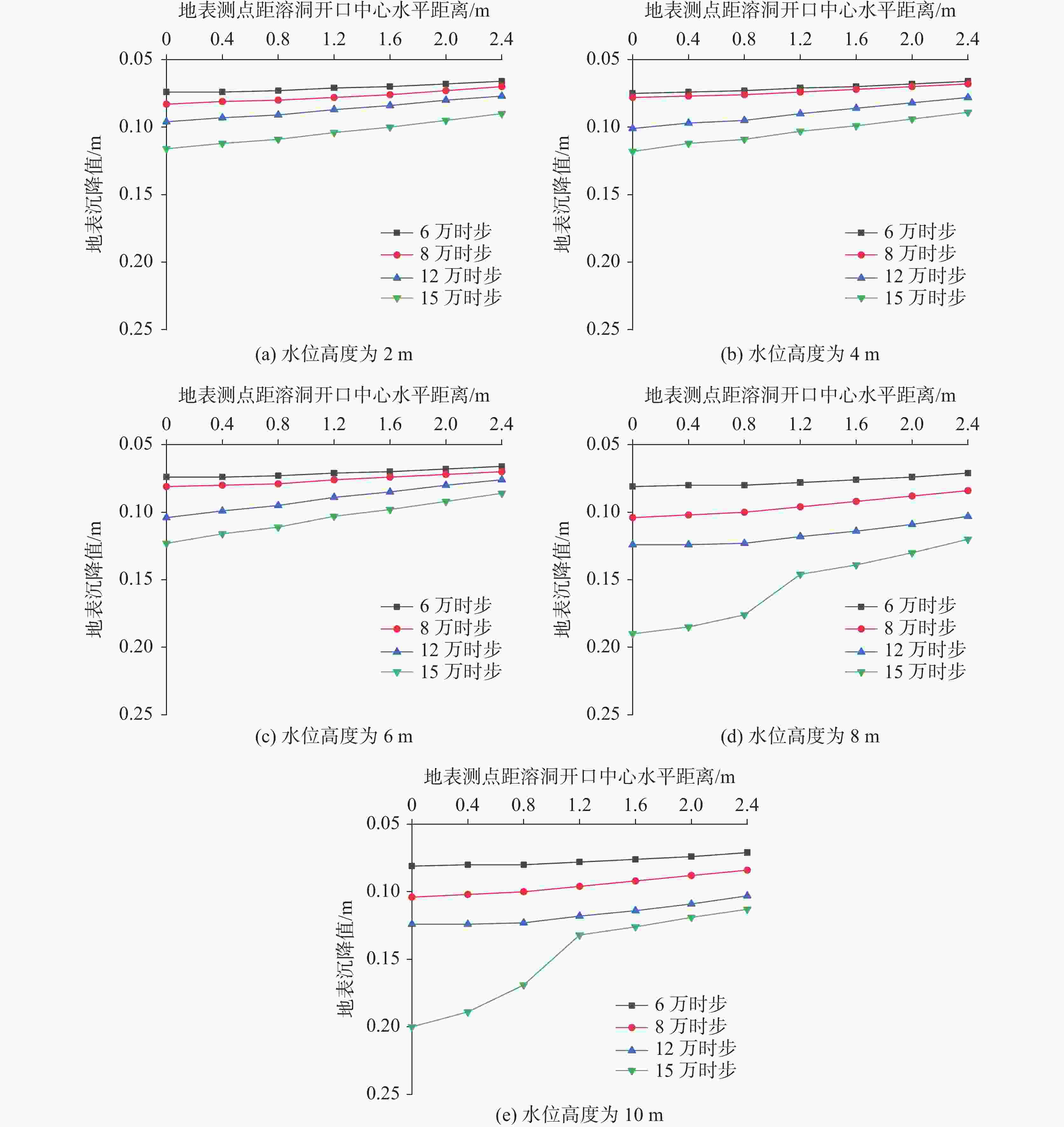
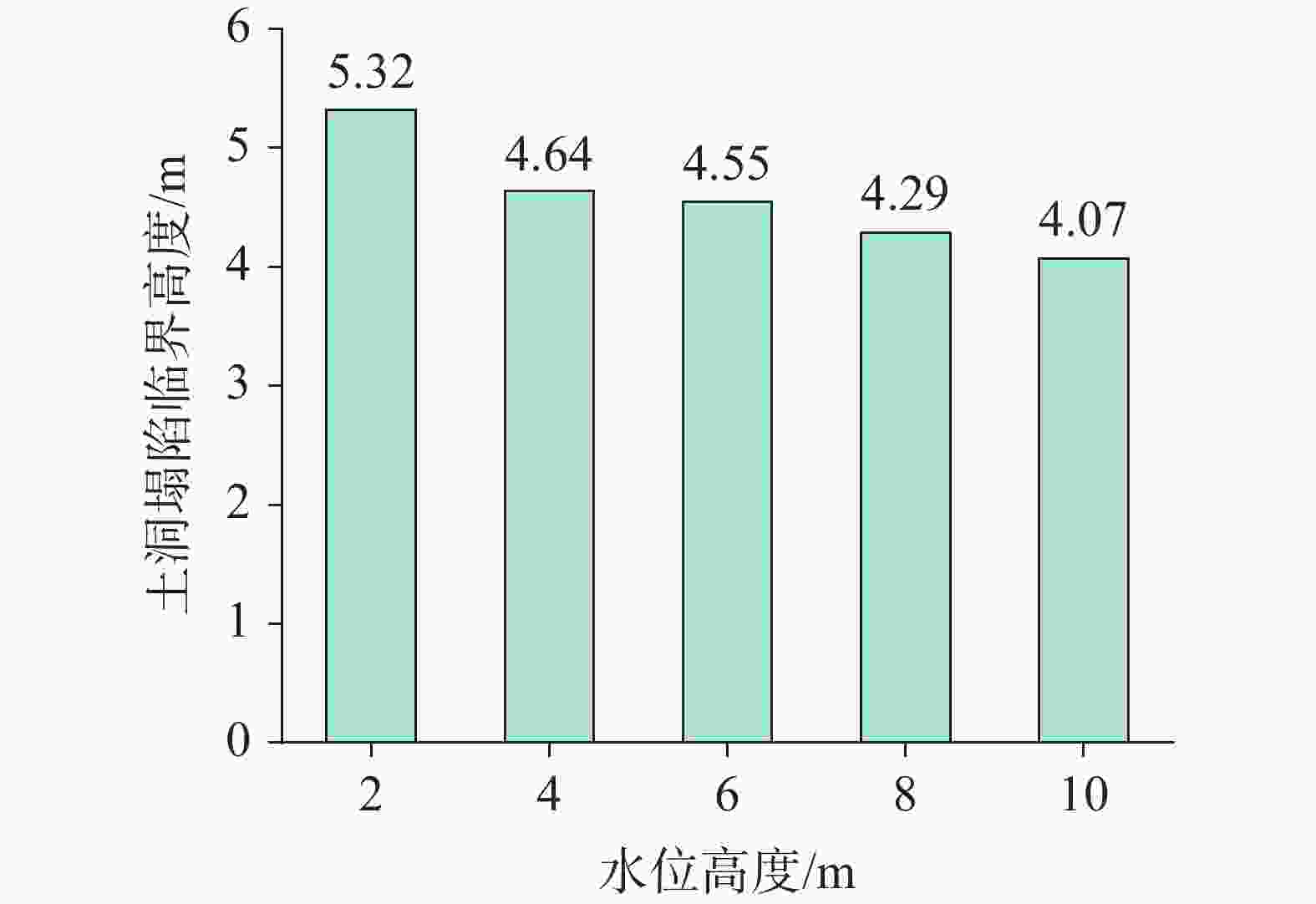
摘要: 为揭示铁路周边覆盖型岩溶土洞扩展的动态演化规律和细观致塌机理，以京沪高铁（江西段）某典型岩溶塌陷点为依托，通过颗粒流（PFC^2D）压缩试验对塌陷土体的强度参数进行标定，引入接触黏结模型，建立覆盖型岩溶地面塌陷流固耦合模型，从细观角度揭示了岩溶地面塌陷的动态演化过程与变形特征，探究不同溶洞开口大小、覆盖层厚度、地下水位高度对覆盖型岩溶地面塌陷变形特征的影响。研究表明：地表沉降、土体孔隙率等随塌陷演化发展而逐渐增大；地下水位高度越高，土洞扩展越快，地表沉降越明显，塌陷也越易发生；溶洞开口越大，地面沉降深度和范围随之增大，塌陷越易发生；覆盖层厚度越小，地表沉降变化越明显；从细观角度可知，塌陷过程中颗粒间接触力变化过程近似为“应力平衡－应力拱形成－应力拱破坏－应力再次平衡－…－应力拱断裂”的规律。研究从细观角度揭示了岩溶地面塌陷演化的全过程，可为高速铁路建设、运营期周围环境覆盖型岩溶地面塌陷的防灾减灾提供参考。
- 覆盖型岩溶 /
- 土洞扩展 /
- 颗粒流 /
- 数值模拟 /
- 动态演化
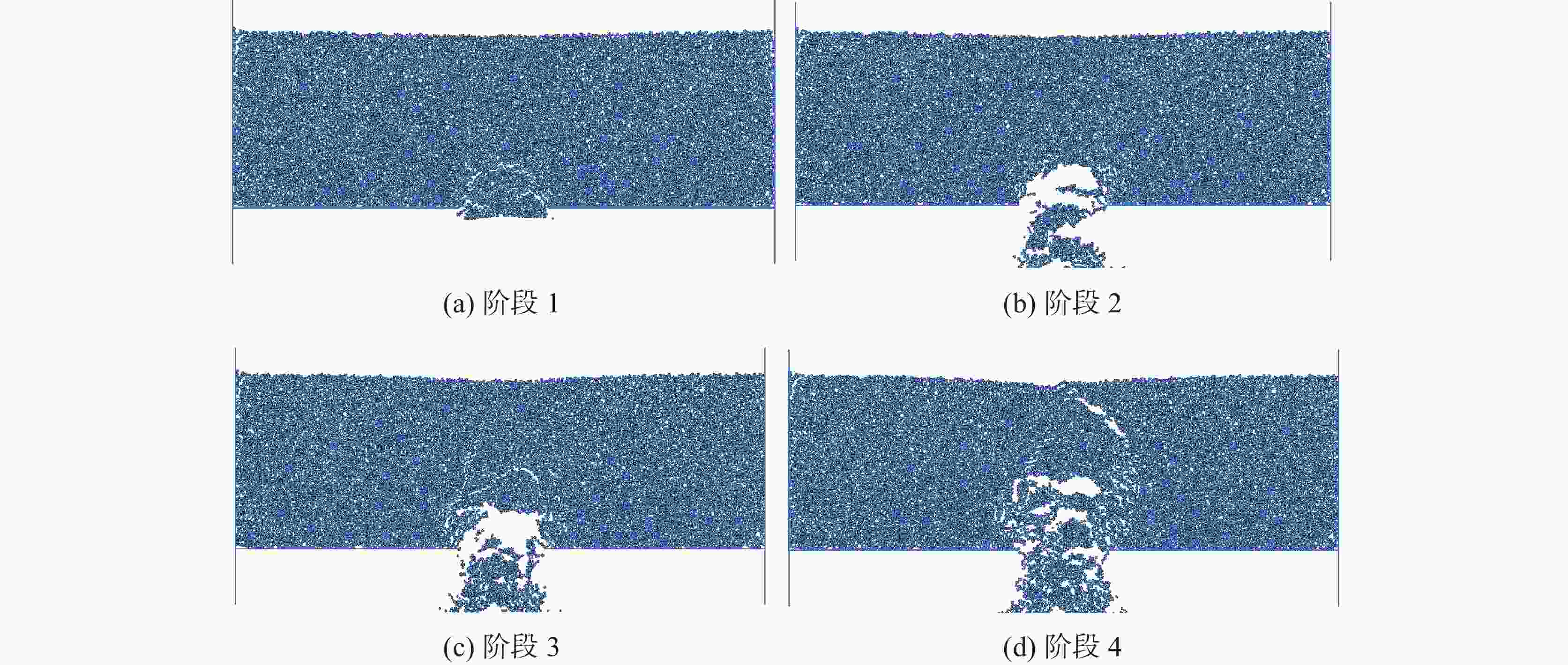
Abstract: Karst collapse represents a significant geological hazard, predominantly occurring in regions characterized by the presence of soluble rock formations, including carbonate rocks, calcareous clastic rocks and salt rocks, among others. The characteristics of karst collapse fall into three key attributes: a hidden spatial distribution, a sudden occurrence and a periodic recurrence over time. These attributes can collectively challenge the construction of major infrastructure in karst areas. A karst collapse disaster along the railway will potentially pose a significant threat to the safe construction and continued operation of the high-speed railways. During both the construction and operational phases of railways in karst areas, pumping and discharging groundwater, along with altering hydrodynamic conditions, have been identified as key factors contributing to karst collapse. The most widely used numerical simulation method is the finite element method (FEM), which is based on the assumption of a continuous medium. FEM simplifies a complex problem by breaking it down into more manageable components. It conceptualizes the solution domain as a collection of small interconnected sub-domains called finite elements. For each element, a suitable (simpler) approximate solution is assumed, and the conditions necessary for solving the overall domain are derived. However, soil is not a continuous medium; therefore, a model based on FEM is unable to simulate the local instability of a collapsed soil body, the damage process at a mesoscopic scale, and other phenomena. In light of the dearth of sufficient attention to the temporal effects and fine-scale mechanisms of the karst collapse process in current studies, this paper aims to elucidate the dynamic evolution laws and mesoscopic-scale collapse mechanisms of the expansion of overlying karst soil caves around the railway.A typical karst collapse site, namely the Beijing–Shanghai high-speed railway (Jiangxi section), was selected as the basis for calibrating the strength parameters of the collapsed soil body. This was achieved through a particle flow (PFC^2D) compression test, in which a contact bonding model was also introduced. This model assumed that the filler in the cave was entirely washed away due to the erosive effect of groundwater seepage. Additionally, the vacuum suction and erosion effect inside the cave were not taken into consideration during the simulation period. The effect of groundwater on soil strength was simulated by reducing the contact strength between particles below the modelled water level. In conclusion, a coupled flow-solid model of overlying karst collapse has been established, which can elucidate the dynamic evolution process and deformation characteristics of karst collapse from a mesoscopic view. Furthermore, the influence of various sizes of cave openings, thicknesses of overburden layers and groundwater levels on the deformation of the overlying karst collapse has been investigated. The migration laws of soil particles under the influence of different factors have been analyzed.The study demonstrates that during the evolution of overlying karst collapse, the contact force between particles undergoes a series of changes, which can be described approximately as follows: equilibrium of stress–formation of stress arch–destruction of stress arch–equilibrium of stress again–…– fracture of stress arch. The internal stress of the soil body demonstrates the following pattern: compressive stress gradually decreasing, tensile stress gradually increasing, and tensile stress disappearing. Additionally, the surface subsidence and porosity of the soil body tend to increase in conjunction with the collapse evolution process. It can be observed that the larger the opening of the cave is, the greater the depth and range of surface subsidence become, which in turn increases the likelihood of collapse. A reduction in the thickness of an overburden layer may cause a more pronounced surface subsidence, thereby increasing the likelihood of collapse. Similarly, an elevated water level may contribute to a more rapid expansion of the soil cave, which in turn will cause a more pronounced surface subsidence and an increased propensity for collapse. The relationship between surface subsidence and thickness of overburden layer is not significant when the thickness of the latter is large. The study provides a comprehensive account of the karst collapse evolution from a mesoscopic perspective, offering insights into prevention and mitigation of karst collapse during the construction and operation of high-speed railways.
- covered karst /
- expansion of soil cave /
- particle flow /
- numerical simulation /
- dynamic evolution

HTML

图 1 研究区岩溶地貌

Figure 1. Karst landform of the study area

下载: 全尺寸图片幻灯片

图 2 潜在塌陷区地层结构剖面图

Figure 2. Profile of the stratigraphic structure of potential collapse area

下载: 全尺寸图片幻灯片

图 3 双轴试验模型

Figure 3. Biaxial test model

下载: 全尺寸图片幻灯片

图 4 模拟的不同围压下应力-应变曲线

Figure 4. Simulated stress-strain curves under different confining pressures

下载: 全尺寸图片幻灯片

图 5 数值计算模型

Figure 5. Numerical model

下载: 全尺寸图片幻灯片

图 6 流固耦合管域模型

Figure 6. Model of pipes and domains for fluid-solid coupling

下载: 全尺寸图片幻灯片

图 7 塌陷全过程模拟

Figure 7. Simulated collapse process

下载: 全尺寸图片幻灯片

图 8 地表竖向位移变化

Figure 8. Vertical displacement of the surface

下载: 全尺寸图片幻灯片

图 9 不同测点处孔隙率随塌陷进程变化规律

Figure 9. Variation of porosity at different monitoring points with collapse process

下载: 全尺寸图片幻灯片

图 10 不同测点塌陷土体内部竖向应力变化曲线

Figure 10. Curve of variation in internal vertical stress of collapsing soil at different monitoring points

下载: 全尺寸图片幻灯片

图 11 不同溶洞开口大小条件下地表沉降变化

Figure 11. Variation of vertical surface displacement under different opening sizes of caves

下载: 全尺寸图片幻灯片

图 12 不同覆盖层厚度条件下地表沉降变化

Figure 12. Variation of vertical surface displacement under different overburden thicknesses

下载: 全尺寸图片幻灯片

图 13 不同水位高度条件下地表沉降变化

Figure 13. Variation of vertical surface displacement under different water levels

下载: 全尺寸图片幻灯片

图 14 不同水位高度突变条件土洞塌陷临界高度

Figure 14. Critical heights of collapsing soil caves under different water levels

下载: 全尺寸图片幻灯片

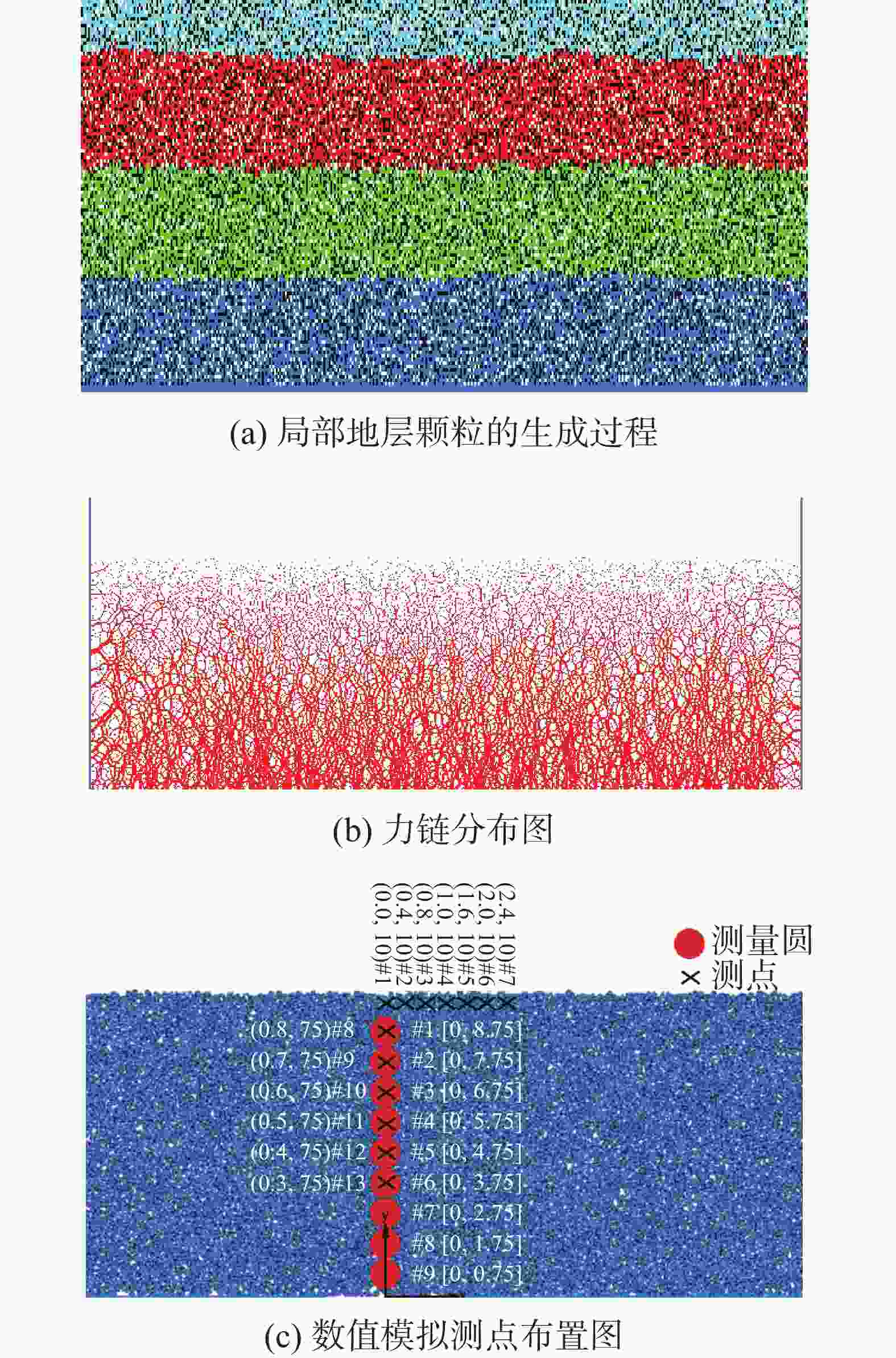
表 1 颗粒流固耦合主要模型参数

Table 1. Main model parameters of particle fluid-solid coupling

岩土层类型	埋深	法向刚度/ MPa·m⁻³	法向-切线刚度比	粘聚力/ kPa	内摩擦角/ °	摩擦系数	容重/ g·cm⁻³	孔隙率/ %
回填土（残坡积粉质黏土）	0−0.5 m	38	1.5	20.5	28.7	0.3	1.68	33
残坡积层粉质黏土	0.5−1.5 m	34	1.5	22.28	25.06	0.3	1.68	32
坡洪积层粉质黏土	1.5−2.5 m	34	1.5	32.54	38.71	0.3	1.69	32
灰岩	>2.5 m	38	1.5	25.47	20	0.3	1.88	28

下载: 导出CSV

参考文献(25)

[1]	宋章, 王科, 蒋良文, 王茂靖. 岩溶区铁路勘察防治技术研究现状及发展趋势[J]. 高速铁路技术, 2018, 9(5):38-43. SONG Zhang, WANG Ke, JIANG Liangwen, WANG Maojing. Research status and developing trends of reconnaissance and control technology of railway in karst area[J]. High Speed Railway Technology, 2018, 9(5): 38-43.
[2]	Bai Haibo, Ma Dan, Chen Zhanqing. Mechanical behavior of groundwater seepage in karst collapse pillars[J]. Engineering Geology, 2013, 164: 101-106.
[3]	高军. 高速铁路岩溶地质路基设计与整治技术[M]. 武汉:中国地质出版社, 2014.
[4]	唐万春, 许模, 于贺艳. 武广客运专线英德段岩溶塌发育规律研究[J]. 地质与勘探, 2011, 47(4):699-704. TANG Wanchun, XU Mo, YU Heyan. Study on karst collapse developing regularity of the Yingde section on the Wuhan-Guangzhou passenger special line[J]. Geology and Exploration, 2011, 47(4): 699-704.
[5]	蒋小珍, 雷明堂, 管振德. 单层土体结构岩溶土洞的形成机理[J]. 中国岩溶, 2012, 31(4):426-432. JIANG Xiaozhen, LEI Mingtang, GUAN Zhende. Formation mechanism of karst soil-void in single-layer soil structure condition[J]. Carsologica Sinica, 2012, 31(4): 426-432.
[6]	蒙彦, 雷明堂. 岩溶塌陷研究现状及趋势分析[J]. 中国岩溶, 2019, 38(3):411-417. MENG Yan, LEI Mingtang. Analysis of situation and trend of sinkhole collapse[J]. Carsologica Sinica, 2019, 38(3): 411-417.
[7]	时刚, 王宇虓, 武天仪, 刘忠玉. 交通荷载下城市路面塌陷问题的试验研究[J]. 地下空间与工程学报, 2020, 16(4):1202-1209. SHI Gang, WANG Yuxiao, WU Tianyi, LIU Zhongyu. Model experiments on ground collapse under traffic roads[J]. Chinese Journal of Underground Space and Engineering, 2020, 16(4): 1202-1209.
[8]	罗小杰, 沈建. 我国岩溶地面塌陷研究进展与展望[J]. 中国岩溶, 2018, 37(1):101-111. LUO Xiaojie, SHEN Jian. Research progress and prospect of karst ground collapse in China[J]. Carsologica Sinica, 2018, 37(1): 101-111.
[9]	Shi H, Bai M Z, Xing S C. Mechanics parameter optimization and evaluation of curtain grouting material in deep, water-rich karst tunnels[J]. Advances in Materials Science and Engineering, 2017, 2017: 1853951.
[10]	Huang Zhen, Zhao Kui, Li Xiaozhao, Zhong Wen, Wu Yun. Numerical characterization of groundwater flow and fracture induced water inrush in tunnels[J]. Tunneling and Underground Space Technology, 2021, 116(9): 104119.
[11]	Shi H, Li Q M, Zhang Q L, Yu Y Z, Xing Y J, Yu K. Mechanism of shallow soil cave-type karst collapse induced by water inrush in underground engineering construction[J]. Journal of Performance of Constructed Facilities, 2020, 34(1): 04019091. doi: 10.1061/(ASCE)CF.1943-5509.0001353
[12]	白明洲, 陈云, 师海. 山岭隧道施工诱发地下水位下降环境风险评价[J]. 铁道工程学报, 2016, 33(1):5-10, 15. BAI Mingzhou, CHEN Yun, SHI Hai. Environmental risk assessment of underground water level falling induced by construction in mountain tunnel[J]. Journal of Railway Engineering Society, 2016, 33(1): 5-10, 15.
[13]	罗小杰, 罗程. 岩溶地面塌陷三机理理论及其应用[J]. 中国岩溶, 2021, 40(2):171-188. LUO Xiaojie, LUO Cheng. Three-Mechanism Theory (TMT) of karst ground collapse and its application[J]. Carsologica Sinica, 2021, 40(2): 171-188.
[14]	吴亚楠. 泰安市城区—旧县水源地岩溶塌陷演化过程分析[J]. 中国岩溶, 2017, 36(1):94-100. WU Ya'nan. Analysis of karst collapse development in Tai'an–Jiuxian water source area[J]. Carsologica Sinica, 2017, 36(1): 94-100.
[15]	王滨, 贺可强. 岩溶塌陷临界土洞的极限平衡高度公式[J]. 岩土力学, 2006(3):458-462. WANG Bin, HE Keqiang. Study on limit equilibrium height expression of critical soil cave of karst collapse[J]. Rock and Soil Mechanics, 2006(3): 458-462.
[16]	雷明堂, 蒋小珍, 李瑜. 岩溶塌陷模型试验:以武昌为例[J]. 地质灾害与环境保护, 1993, 4(2):39-44.
[17]	吴庆华, 张伟, 刘煜, 崔皓东. 基于物理模型试验的岩溶塌陷定量研究[J]. 长江科学院院报, 2018, 35(3):52-58. WU Qinghua, ZHANG Wei, LIU Yu, CUI Haodong. Quantifying the process of karst collapse by a physical model[J]. Journal of Yangtze River Scientific Research Institute, 2018, 35(3): 52-58.
[18]	马荣和, 许汉华, 赵毅然. 个旧市木登硐村岩溶场地稳定性数值模拟[J]. 中国水运(下半月), 2019, 19(10):104-106.
[19]	陈冬琴, 唐仲华, 陈锐. 基于水动力-力学耦合方法的岩溶塌陷预测[J]. 安全与环境工程, 2016, 23(4):26-32. CHEN Dongqin, TANG Zhonghua, CHEN Rui. Prediction of karst collapse based on hydrodynamic-mechanical coupling method[J]. Safety and Environmental Engineering, 2016, 23(4): 26-32.
[20]	贾龙, 蒙彦, 管振德. 岩溶土洞演化及其数值模拟分析[J]. 中国岩溶, 2014, 33(3):294-298. JIA Long, MENG Yan, GUAN Zhende. Evolution and numerical simulation of a karst soil cave[J]. Carsologica Sinica, 2014, 33(3): 294-298.
[21]	于林弘, 颜嘉良, 于晓静, 扈胜涛. 基于FLAC^3D的岩溶土洞演化及数值模拟分析[J]. 地下水, 2020, 42(4):55-57. YU Linhong, YAN Jialiang, YU Xiaojing, HU Shengtao. Evolution and numerical simulation of karst caves based on FLAC^3D[J]. Ground Water, 2020, 42(4): 55-57.
[22]	石崇, 张强, 王盛年. 颗粒流(PFC5.0)数值模拟技术及应用[J]. 岩土力学, 2018, 39(Suppl.2):36-39. SHI Chong, ZHANG Qiang, WANG Shengnian. Particle flow (PFC5.0) numerical simulation technology and its application[J]. Rock and Soil Mechanics, 2018, 39(Suppl.2): 36-39.
[23]	何树江. 基于颗粒流的灰岩细观力学参数标定方法及其敏感性分析[D]. 济南:山东大学, 2018. HE Shujiang. Calibration method and sensitivity analysis of micromechanic parameters for limestone based on particle flow[D]. Jinan: Shandong University, 2018.
[24]	周建, 张映钱, 方亿刚, 刘宇. 水位变动及降雨入渗联合作用对岩溶地面塌陷的影响分析[J]. 水利与建筑工程学报, 2016, 14(1):218-222. ZHOU Jian, ZHANG Yingqian, FANG Yigang, LIU Yu. Analysis of joint action of water level fluctuation and rainfall on the influence of karst ground collapse[J]. Journal of Water Resources and Architectural Engineering, 2016, 14(1): 218-222.
[25]	姚玉相. 基于离散单元法的高填黄土减载明洞土拱效应细观数值模拟研究[D]. 兰州:兰州交通大学, 2020. YAO Yuxiang. Analysis on meso-mechanism of soil arching for unloading structure of high-filled cut-and-cover tunnel based on DEM[D]. Lanzhou: Lanzhou Jiaotong University, 2020.