Structure and application of SWAT-MODFLOW coupling model for surface-groundwater
-
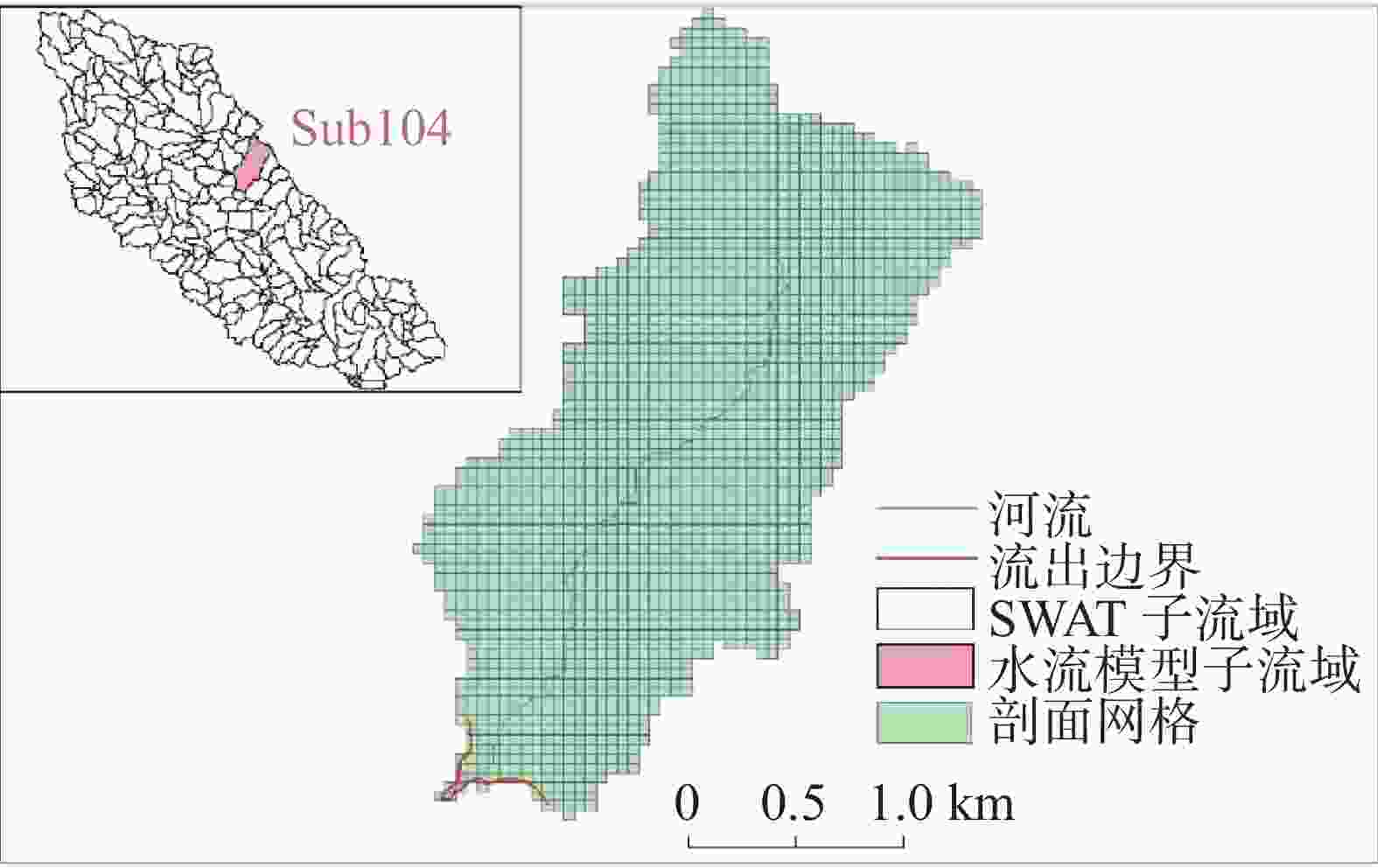
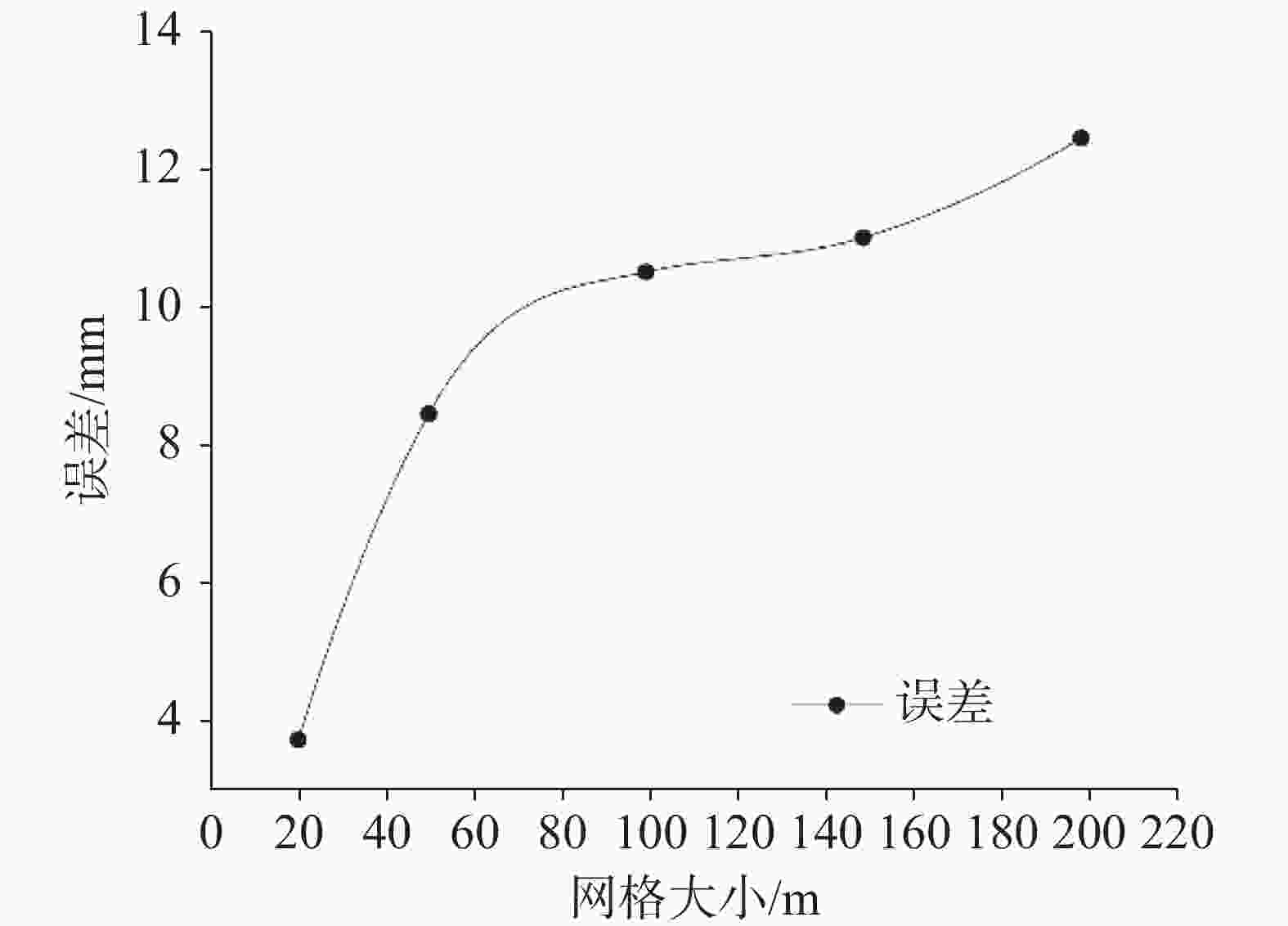
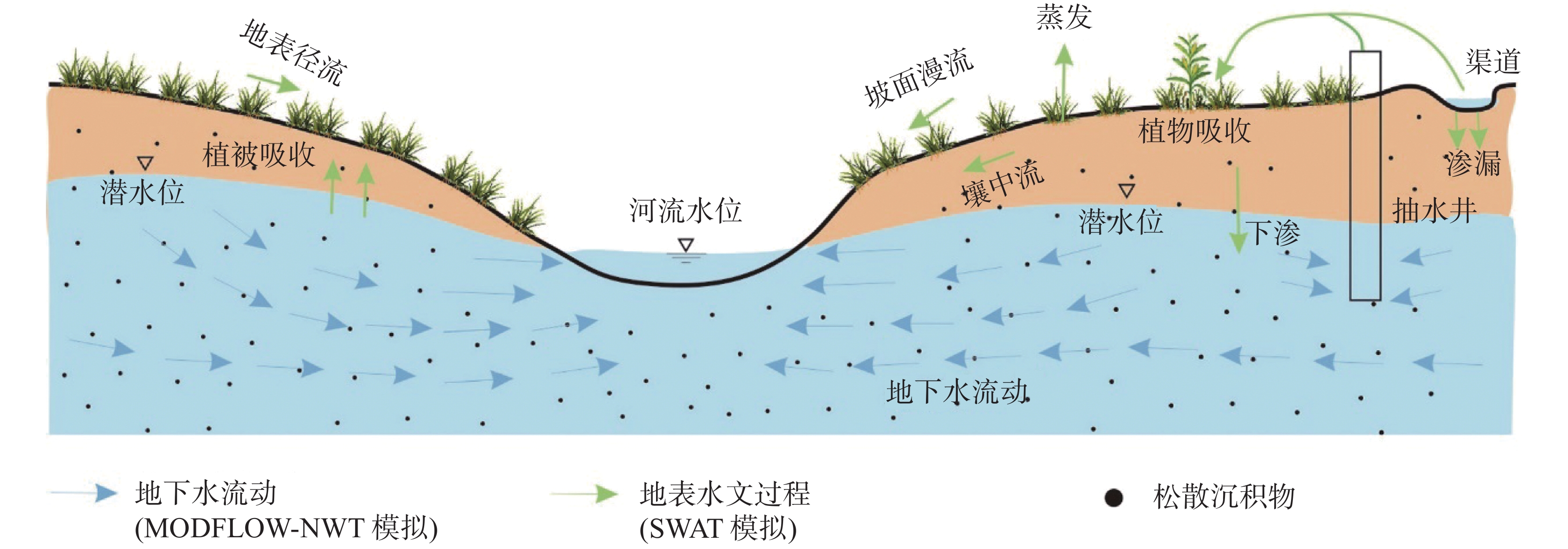
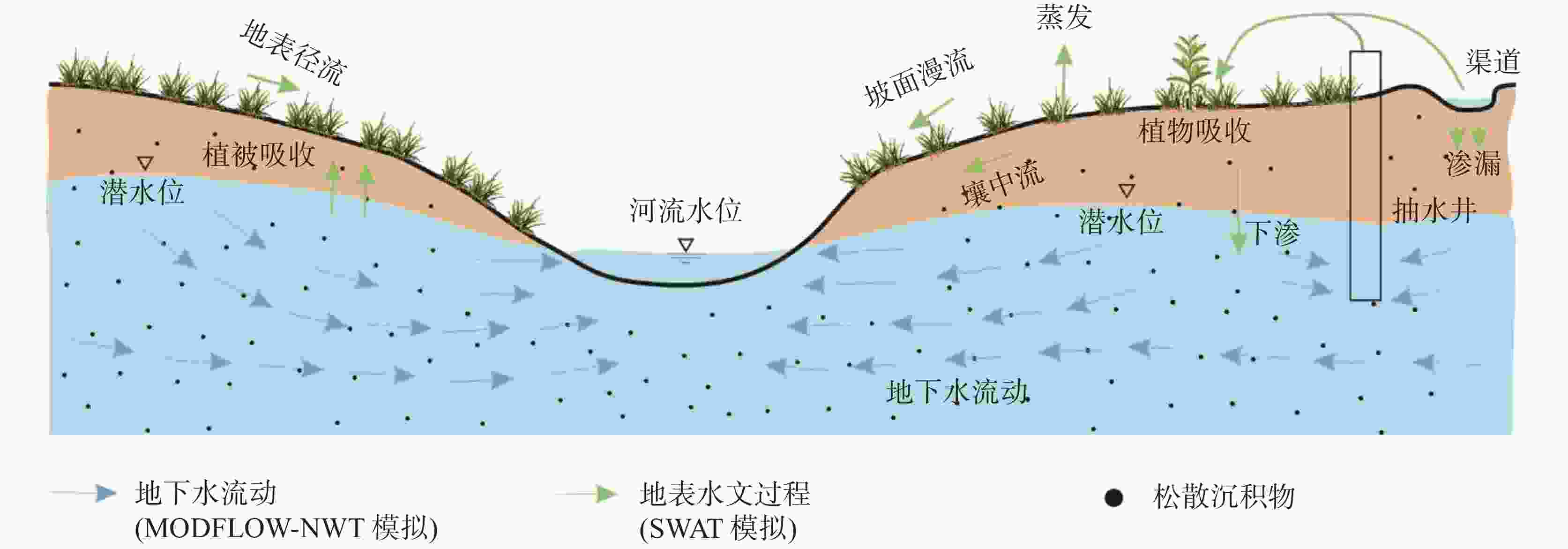
摘要: 为了利用Seonggyu Park和Ryan T.Bailey的SWAT-MODFLOW耦合程序实现地表、地下不同范围模型耦合，同时探究耦合程序输出的以SWAT计算的地下水补给量和以MODFLOW网格计算的补给量之间的差异，以及耦合程序在有关地表地下水研究上的优势。本文以该耦合程序示例模型美国佐治亚州南部小河流域（LRW）为例，选取模型中SWAT划分的104号子流域为边界，用GMS10.4建立地下水流模型，最后将地下水流模型和原SWAT模型进行耦合。研究结果表明：(1)耦合程序能实现以地表分水岭自然边界为范围的SWAT模型与以子流域为边界的小范围MODFLOW模型的耦合，但由于地下水流模型网格边界和子流域边界不能完全匹配，导致MODFLOW以网格计算的地下水降雨补给量和SWAT统计的地下水降雨补给量存在差异，误差随网格变小而变小；(2)耦合后各均衡项发生了变化，河道对地下水的总补给量变为耦合前的15.25%，地下水向河道的总排泄量比耦合前多19.29%，总降雨补给比耦合前多17.07%，总蒸发量是耦合前的3.08倍。经过研究发现耦合模型能更准确的模拟地表地下水文过程，反映降水与地下水、地表水与地下水转化关系。
-
关键词:
- SWAT-MODFLOW /
- 耦合模型 /
- 地表−地下水
Abstract:Surface water and ground water is a unified whole in the water circulation system, and there is a close relationship between them. Especially in the areas where karst surfaces such as drop holes and funnels are developed, surface water and groundwater can form a direct connection. The interactions between surface water and groundwater have been a hot topic in research. A great deal of research has been carried out both nationally and internationally. The SWAT-MODFLOW coupling procedure developed by Seonggyu park and Ryan T. Peley is a beneficial tool for studying surface-groundwater interactions. This coupling procedure establishes the link between the Hydrological Response Unit (HRUs) in SWAT model and the spatial grid in MODFLOW through the ARCGIS platform in order to achieve a loose coupling of the model. A number of applications of this program have been carried out abroad. However, no relevant studies have used this procedure to achieve model coupling in different ranges of surface and subsurface. As far as the actual situation is concerned, often the plains are the focus of extraction and their groundwater dynamic field needs to be detailed delineated. However, the scope of SWAT model covers the overall basin, which is not consistent with the scope of groundwater flow model. Considering the running time and the accuracy of the model, it is necessary to explore the model coupling process in different ranges of surface-groundwater. In this study, the SWAT-MODFLOW coupling program of Seonggyu park and Ryan T. Bailey was used to implement the coupling of models at different scales of the surface and subsurface, and to investigate the differences between the groundwater recharge calculated in SWAT and that calculated in the MODFLOW grid output of the coupling program. Then the advantages of the coupling program for relevant studies on surface water and groundwater were analyzed. Taking this coupling procedure model of the Little River Watershed (LRW) in southern Georgia, USA as an example, this study selected Sub-basin 104 divided by the SWAT in the model as the boundary, and built the groundwater flow model with GMS10.4 based on the data of the original example model. According to the coupling model manual, ARCGIS platform and EXCEL platform, four link files required by the coupling model were completed: swatmf_dhru2grid, swatmf_dhru2hru, swatmf_grid2dhru, and swatmf_river2grid. A coupling model of Sub-basin 104 water flow model and the overall SWAT model was further developed, and the format of the model output results was controlled through its link files. On the basis of calculation results of the model, its multi-year equilibrium condition was calculated in EXCEL to judge its rationality so that the model can be calibrated. After the calibration, the accuracy of each equilibrium item was compared between the coupling model and the independent groundwater flow model. Study results show as follows. (1) The coupling procedure enables the coupling of the SWAT model naturally bounded by the surface watershed with the small-scale MODFLOW model divided by the sub-basin boundary. However, because the grid boundary of the groundwater flow model and that of sub-basin cannot be completely matched, there is a difference between MODFLOW and SWAT in terms of the calculation of rainfall recharge for groundwater. In general, the calculation volume of SWAT is larger than that of MODFLOW grid. The calculations clearly indicate that the error margin becomes smaller as the grid gets smaller because the smaller the grid area is, the more exact the match between the grid and the boundary becomes. (2) Each equilibrium item has changed after coupling. Because the river depth in GMS is taken as the empirical value, and it is taken as the confluence evolution value in SWAT, calculations show that the groundwater recharge of the river before and after the model coupling is significantly different, and the total recharge from the river to the groundwater reduces to 15.25% of that before the coupling. On the other hand, the total discharge from groundwater to river increases 19.29% after coupling. The rainfall recharge of the model before coupling is calculated by infiltration coefficient method, and the groundwater recharge after coupling is the seepage of the soil bottom of the SWAT model. The calculations show that the total rainfall recharge increases 17.07% after coupling. The groundwater evaporation before model coupling is calculated by the Avyanov formula, and the groundwater evaporation after coupling was calculated according to the potential evapotranspiration and the actual evapotranspiration calculated by SWAT. The calculations show that the total evapotranspiration is 3.08 times larger than that before coupling. It is found that the coupling model can simulate the surface-subsurface hydrological process more accurately, and can reflect the relationship between precipitation and groundwater, surface water and groundwater transformation. -
Key words:
- SWAT-MODFLOW /
- coupling model /
- surface-groundwater
-
0. 引 言
数值模型是定量分析水文过程的重要工具，其中具代表性的模拟软件有SWAT和MODFLOW。SWAT是一种半分布式地表水文模型[1]，较好地考虑了众多因素的空间异质性，因此在众多学者的应用中都取得了不错效果，包含农业区污染物运移[2,3]、生态补水[4-6]、径流模拟[7-12]、水资源评价[13-14]、人为管理活动对水文要素的影响[15-16]等。SWAT聚焦于对地表径流和河道汇流刻画，用SCS曲线法或Green&Ampt下渗法模拟地表径流，用蓄水量变化法或马斯京根法计算河道汇流，用曼宁公式计算流速。但SWAT对地下水的考虑比较简单，无法刻画地下水流场的时空变化。MODFLOW模型能够较好地模拟研究区多含水岩组的非均质性特征，在国内外广泛应用，主要包括：地下水资源量评价[17-19]、地下水污染分析[20]、矿坑涌水量预测[21]等。MODFLOW主要适用于松散介质含水层地下水流动模拟，在岩溶发育较弱的地区，可将含水介质看成等效多孔介质用MODFLOW进行处理[22-29]，在岩溶发育较强烈的地区模拟效果欠佳。在实际应用中，往往需要精细刻画重点区域的地下水动力场，即地下水模型的范围不是与SWAT对应的完整流域，为了更准确地描述地表地下水交换规律，需要探索流域大范围SWAT模型与区域小范围MODFLOW模型耦合的实现过程。
根据模型耦合方法的不同，耦合模型可以分为全耦合和松散耦合。全耦合是指控制地表和地下水流动的方程可以在一个软件包内同时得到求解，而松散耦合是指两个或多个模型通过交换模型求解结果的方式耦合在一起。张琳琳等[30]通过传递SWAT模型结果的方式实现了模型的松散耦合，探讨了耦合模型对地下水补给量和山前侧向补给量精度的提升，为地下水均衡分析提供了更有效的手段。SWAT-MODFLOW耦合程序是2016年Seonggyu Park和Ryan T.Bailey开发的将SWAT和MODFLOW-NWT耦合在一起的松散耦合程序。该模型在研究地表地下水综合性较强的问题上具有独到的优势[31]。国内外学者已经基于该耦合程序开展了一些研究。例如气象要素和灌溉活动对地下水的影响[32]、地表水或土壤水与地下水之间的转化规律[33-36]、水资源的优化配置[37-38]、在一些地表水和地下水存在较强交互现象的地区探究地下水对河流补给的时空特征[39]、在地势比较低洼的农业地区研究地下排水工程对地下水文过程的影响[40]，目前的研究对地表−地下水时空转化规律的认识尤为关注。由于模型公布的时间不长，该耦合程序的应用尚不多见，关于用该程序实现地表地下不同模型范围耦合的应用还处于空白。
本文基于Seonggyu Park和Ryan T.Bailey的SWAT-MODFLOW耦合程序示例模型[41]，尝试选取SWAT划分的104号子流域，用该示例模型数据插值建立地下水模型，实现了SWAT-MODFLOW耦合程序在地表地下水不同研究区范围的耦合，对比分析了地下水流模型网格剖分大小对地下水补给量计算结果的影响，并以此为基础总结了耦合模型的特点及优势。
1. 耦合模型原理
1.1 水文过程及传递的变量
耦合模型各自模拟的水文过程如图1所示[29-31]。SWAT模拟地表径流的产生及汇流、土壤水的下渗及植物水分吸收、以及河流汇流及湖泊湿地储水下渗及蒸发等水文过程。MODFLOW模拟各含水层地下水的流动以及地下水和地表水的交换量计算。模型均衡方程如式1所示。
GWSTOR=R补给−D排泄 (1) R补给=RECH+SWGW+GWCON (2) D排泄=GWQ+DRN+GWET (3) 式中：GWSTOR为含水层储存变化量，mm；RECH为SWAT中HRUs补给量，mm；SWGW为河流渗漏量，mm；GWCON为边界流入量，mm；GWQ为含水层向河流排泄量，mm；DRN为含水层向排水沟的排泄量，mm；GWET为潜水蒸发量，mm。如有其他均衡项，须另外补充进方程。
SWAT-MODFLOW的运行需要以下四个状态变量（表1）在SWAT和MODFLOW模型之间传递。基于ARCGIS平台将SWAT的HRUs分解为DHRUs，DHRUs按照空间位置和MODFLOW对应的网格进行关联，以便进行降雨、蒸发、河流水位以及地表水和地下水交换速率等变量在两个模型间的传递。
表 1 SWAT-MODFLOW传递变量说明表Table 1. Variables passed by SWAT-MODFLOW变量 传递方式 说明 潜水的补给量 水文响应单元到地下水流模型
对应活动网格地下水补给由SWAT计算 蒸发 水文响应单元到地下水流模型
对应活动网格SWAT计算的潜在蒸散发和实际蒸
散发的差值由潜水继续蒸发子流域河道的水位 SWAT计算的河道水位到地下
水流模型河流网格地下水流模型的河流网格水位由
SWAT计算的河道水位而定地下水和河流的交换量 地下水流模型河流网格计算结果到
SWAT子流域河道交换量由River包计算后传递给
SWAT模型河道1.2 耦合程序对地下水流模型数据的替换
耦合程序会将MODFLOW原模型的一些输入数据替换为SWAT模拟的结果。MODFLOW须用River包模拟研究区内的河流，River包中的河道水位高程会根据SWAT计算的河道水深自动替换。对于地下水流模型的降雨补给，当网格接受SWAT水文响应单元计算的地下水补给时，原Recharge包中的数据会被重写。对于模型的蒸发，耦合程序自动将网格的蒸发高程设置成地表高程，最大蒸发速率为SWAT计算的潜在蒸散发和实际蒸散发的差值，称为剩余蒸发量ETresidual。
2. 应 用
2.1 流域基本条件
小河流域[42]是美国区域性的试验流域，位于乔治亚州南部苏旺尼河流域源头地区。该研究区对沿海平原地区的土壤、地层、气候以及农业生产情况都具有一定的代表性。土地利用类型主要为森林、农田、牧场、湿地等，其所占比例见表2。由表中可见流域森林覆盖面积较广，占总面积的65%，其次为农田，占总面积的30%。该流域多年平均降雨量约为1 200 mm，具有降雨时间短，降雨强度大的特点。流域为一处冲积平原、河流阶地，面积约为334 km2。河道坡度一般小于0.1%，上游近似为5%。山谷底部近似水平，坡度值小于5%，山谷两侧坡度较缓，坡度值于5%~15%之间。地表主要覆盖有砂或砂壤土，渗透性较好，渗透系数一般大于1.2 m∙d−1，厚度2~10 m。下覆石灰岩含水层，河床切入含水层较浅。潜水含水层和河流交换量受季节变动影响。
表 2 小河流域土地利用类型Table 2. Land use types in the small river basin类型 森林 农田 牧场 湿地 其它 比例/% 65 30 2 2 1 2.2 耦合模型
流域总面积331.88 km2，基于汇水面积阈值控制，SWAT将流域划分为240个子流域，如图2所示。通过研究区土地利用、土壤类型和坡度分级的组合，剔除不满足条件的水文响应单元（HRUs）后，全区共生成6 233个水文响应单元，模拟期为1988到2001年。预热期为5年。
图 2 选取的子流域及地下水流模型网格剖分示意图Figure 2. Grid partition diagram of selected sub-basin and groundwater flow model为了验证耦合程序在改变地下水流模型范围下的适用性，及考虑到子流域面积不宜过小。地下水流模型选取SWAT划分的104号子流域为范围，该子流域共划分49个HRUs，地表分布砂及砂壤土，下覆石灰岩，岩性分布较为均一。因为SWAT根据地形划分子流域，认为地表分水岭和地下水分水岭近似相同，所以地下水流模型四周边界为隔水边界，在子流域出口处地形较为平坦，根据地下水流场方向假设为流出边界。含水层划分为1层。模型的输入项为降雨、河流，输出项为蒸发、河流、流出边界。网格剖分大小为100 m×100 m，模拟期为1988到2001年，地下水模型以月为应力期。
将SWAT模型和地下水流模型建立好后，基于ARCGIS平台和EXCEL按照建模流程构建耦合模型。
3. 结果分析
3.1 网格剖分对模型精度的影响
地下水流模型不再是与SWAT对应的流域范围上的模型，而是单独耦合了某个子流域，由于在边界上HRUs和网格匹配的问题，影响了地下水的补给量计算。为了探究地下水流模型网格剖分大小对地下水补给量的影响，设置了六组情景进行模拟，分别为原始全范围耦合模型、和五组单独耦合104号子流域模型。单独耦合104号子流域网格大小为20 m×20 m、50 m×50 m、100 m×100 m、150 m×150 m、200 m×200 m，第六组为原始全范围耦合模型。如表3给出了六种情景下SWAT模型、MODFLOW计算地下水补给量的结果对比，误差计算公式如式4。
表 3 地下水补给量误差分析列表（单位：mm）Table 3. Error analysis of groundwater recharge (unit: mm)组号 网格大小/m 项 1993 1994 1995 1996 1997 1998 1999 2000 2001 平均 SWAT 281.92 417.84 148.54 160.65 322.96 229.36 103.80 254.44 231.60 239.01 1 20 MODFLOW 277.01 412.20 146.30 157.71 314.76 228.73 102.64 245.75 232.56 235.30 误差 4.90 5.64 2.24 2.94 8.20 0.64 1.16 8.69 −0.96 3.72 2 50 MODFLOW 271.41 403.84 143.32 154.49 308.43 224.15 100.54 240.94 227.76 230.54 误差 10.51 14.00 5.22 6.16 14.53 5.21 3.26 13.50 3.85 8.47 3 100 MODFLOW 269.05 400.40 142.06 152.90 305.76 222.08 99.51 238.67 225.79 228.47 误差 12.86 17.44 6.47 7.76 17.20 7.28 4.28 15.78 5.81 10.54 4 150 MODFLOW 268.40 399.20 141.52 153.27 304.61 221.38 99.67 238.34 225.41 227.98 误差 13.52 18.64 7.02 7.38 18.35 7.99 4.13 16.10 6.19 11.04 5 200 MODFLOW 266.75 396.80 141.05 152.21 302.59 220.05 99.17 235.66 224.41 226.52 误差 15.17 21.04 7.49 8.44 20.37 9.31 4.63 18.78 7.19 12.49 6 200 MODFLOW 283.49 418.63 150.37 158.93 320.69 236.38 104.96 238.88 241.06 239.27 误差 0.69 0.52 −0.14 0.86 1.37 −0.86 0.15 0.93 0.04 0.40 Erch=PERC−RCHmf (4) 式中：Erch为地下水降雨补给误差，mm；PERC为SWAT中HRUs计算的地下水补给量，mm；RCHmf为MODFLOW计算的地下水降雨补给量，mm。
六组情景9年的模拟结果表明，一般情况下SWAT计算的进入潜水含水层的水量（PERC）要稍大于该耦合程序计算的潜水含水层网格补给量。当耦合104号子流域地下水流模型时，从图3中可以看出，网格越大，两者的误差也越大，当网格边长为200 m时，平均误差达到最大，为12.49 mm，占潜水补给量的5.5%。对比第6组情景和前5组情景可以看出，当地下水流模型以全流域为范围时，地下水潜水的补给误差最小为0.4 mm，占地下水补给量的0.16%，几乎无误差。
图 3 地下水补给量误差随网格大小的变化曲线Figure 3. Variation curve of groundwater recharge error with the change of grid sizes3.2 耦合模型对均衡项精度的提升
模型的精度除受网格大小影响外还受其他多种因素影响，若网格过小，研究精度和模型计算工作量及时间也会增长，因此在确定网格大小时要综合考虑各种因素。考虑到地下水模型范围的大小和网格剖分带来的地下水补给误差，选取网格100 m×100 m与SWAT模型进行了耦合，对比分析了耦合模型相对单一地下水流模型在地表地下水交换计算量上的区别，模型均衡表如表4、表5。
表 4 耦合前地下水流模型均衡表（单位：104 m3）Table 4. Equalization table of groundwater flow model before coupling (unit: 104 m3)项 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 流入 河流 6.00 5.39 5.42 3.96 4.46 4.47 4.05 4.44 5.06 4.90 4.19 5.15 5.28 4.61 降雨 95.51 106.89 99.73 132.19 105.53 109.14 141.48 80.55 94.97 119.34 105.56 77.89 105.85 101.00 总流入 101.51 112.28 105.15 136.15 109.99 113.61 145.53 84.99 100.03 124.24 109.76 83.04 111.14 105.60 流出 边界 36.60 36.50 36.5 36.50 36.60 36.50 36.50 36.50 36.60 36.50 36.50 36.50 36.50 36.50 河流 60.57 65.39 64.70 84.31 76.81 75.97 85.22 79.15 67.58 68.91 80.96 65.22 64.40 72.41 蒸发 0.34 0.37 0.36 0.49 0.44 0.43 0.49 0.45 0.37 0.38 0.46 0.36 0.36 0.41 总流出 97.51 102.26 101.57 121.30 113.85 112.90 122.21 116.10 104.55 105.80 117.92 102.08 101.36 109.32 均衡 4.00 10.02 3.58 14.85 −3.86 0.71 23.32 −31.11 −4.52 18.44 −8.16 −19.05 9.77 −3.71 总均衡 14.28 表 5 耦合后地下水流模型均衡表（单位：104m3）Table 5. Equilibrium table of groundwater flow model after coupling (unit: 104m3)项 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 流入 河流 0.75 0.99 0.76 0.70 0.57 0.65 0.64 0.43 0.70 0.93 0.54 0.72 1.11 0.78 降雨 102.80 109.61 87.05 214.65 135.54 141.00 209.76 74.45 80.33 160.17 116.36 52.15 125.39 118.29 总流入 103.54 110.59 87.82 215.35 136.12 141.65 210.39 74.88 81.02 161.1 116.90 52.87 126.50 119.07 流出 边界 36.60 36.5 36.50 36.50 36.60 36.50 36.50 36.50 36.60 36.50 36.50 36.50 36.60 36.50 河流 81.98 59.20 71.96 117.54 101.81 100.52 118.00 107.79 70.73 70.99 107.99 60.90 55.20 82.76 蒸发 1.05 0.66 1.10 1.92 1.50 1.57 1.61 1.83 0.99 0.89 1.82 0.81 0.68 1.23 总流出 119.62 96.36 109.57 155.96 139.91 138.58 156.11 146.12 108.32 108.38 145.73 98.21 92.49 120.49 均衡 −16.08 14.24 −21.75 59.39 −3.80 3.06 54.28 −71.24 −27.29 52.72 −28.82 −45.34 34.01 −1.42 总均衡 1.96 从表4、表5中可知，耦合模型对地下水流模型均衡项的改变显而易见。耦合后地下水流模型的河道水深由SWAT的日计算结果决定，而非耦合前GMS的插值结果，所以河水对地下水的补给和排泄前后有所变化，耦合后河道对地下水的补给总量是耦合前的15.25%，为10.27×104 m3。同时，耦合后地下水向河道的总排泄量比耦合前多19.29%，为1 206.79×104 m3。年际间河道对地下水的补排规律较为一致。
因为模型耦合后地下水的降雨补给量为SWAT计算的土壤剖面底部的渗出量，水文响应单元和网格一一对应，考虑了地表及土壤水文过程，所以相对降雨入渗系数法得到了改善。从表4、表5中可知，1988年到2001年通过降雨入渗系数法计算的地下水降雨总补给量为1 475.63×104 m3，耦合后计算的总补给量为1 727.54×104 m3，比耦合前多17.07%。
SWAT模型计算流域中每个水文响应单元的潜在蒸散发（PET）和实际蒸散发（AET），PET和AET的差值为剩余蒸发能力。当剩余蒸发能力大于零时，若地下水位在极限埋深以上，则以该剩余蒸发能力为最大蒸发速率继续蒸发地下水。由表4、表5可知，耦合后地下水流模型的总蒸发量是耦合前的3.08倍，耦合前后年际间的变化一致。
4. 结 论
本论文探究了Seonggyu Park和Ryan T.Bailey的SWAT-MODFLOW耦合程序在地表地下水交换规律上的应用和特点，得出以下结论：
（1）将地下水流模型范围改变为SWAT划分的某一子流域后模型仍可运行，但由于地下水流模型网格边界和子流域边界不能完全匹配，导致MODFLOW以网格计算的地下水降雨补给量和SWAT统计的地下水降雨补给量存在误差，误差随网格变小而变小，在本文中当网格大小为150 m×150 m时，误差下降到5%以下；
（2）地下水流模型耦合后相比耦合前均衡项均发生了改变。耦合后河道对地下水的总补给量变为耦合前的15.25%，地下水向河道的总排泄量比耦合前多19.29%，总降雨补给比耦合前多17.07%，总蒸发量是耦合前的3.08倍。通过对比，耦合模型在地表水与地下水转化方面、降水对地下水补给入渗方面更可反映实际条件。
耦合模型和地表地下水的转化问题一直是研究热点，本文对有关地表地下水耦合模型的研究具有重要参考意义。
-
图 2 选取的子流域及地下水流模型网格剖分示意图
Figure 2. Grid partition diagram of selected sub-basin and groundwater flow model
图 3 地下水补给量误差随网格大小的变化曲线
Figure 3. Variation curve of groundwater recharge error with the change of grid sizes
表 1 SWAT-MODFLOW传递变量说明表
Table 1. Variables passed by SWAT-MODFLOW
变量 传递方式 说明 潜水的补给量 水文响应单元到地下水流模型
对应活动网格地下水补给由SWAT计算 蒸发 水文响应单元到地下水流模型
对应活动网格SWAT计算的潜在蒸散发和实际蒸
散发的差值由潜水继续蒸发子流域河道的水位 SWAT计算的河道水位到地下
水流模型河流网格地下水流模型的河流网格水位由
SWAT计算的河道水位而定地下水和河流的交换量 地下水流模型河流网格计算结果到
SWAT子流域河道交换量由River包计算后传递给
SWAT模型河道
下载: 导出CSV
表 3 地下水补给量误差分析列表（单位：mm）
Table 3. Error analysis of groundwater recharge (unit: mm)
组号 网格大小/m 项 1993 1994 1995 1996 1997 1998 1999 2000 2001 平均 SWAT 281.92 417.84 148.54 160.65 322.96 229.36 103.80 254.44 231.60 239.01 1 20 MODFLOW 277.01 412.20 146.30 157.71 314.76 228.73 102.64 245.75 232.56 235.30 误差 4.90 5.64 2.24 2.94 8.20 0.64 1.16 8.69 −0.96 3.72 2 50 MODFLOW 271.41 403.84 143.32 154.49 308.43 224.15 100.54 240.94 227.76 230.54 误差 10.51 14.00 5.22 6.16 14.53 5.21 3.26 13.50 3.85 8.47 3 100 MODFLOW 269.05 400.40 142.06 152.90 305.76 222.08 99.51 238.67 225.79 228.47 误差 12.86 17.44 6.47 7.76 17.20 7.28 4.28 15.78 5.81 10.54 4 150 MODFLOW 268.40 399.20 141.52 153.27 304.61 221.38 99.67 238.34 225.41 227.98 误差 13.52 18.64 7.02 7.38 18.35 7.99 4.13 16.10 6.19 11.04 5 200 MODFLOW 266.75 396.80 141.05 152.21 302.59 220.05 99.17 235.66 224.41 226.52 误差 15.17 21.04 7.49 8.44 20.37 9.31 4.63 18.78 7.19 12.49 6 200 MODFLOW 283.49 418.63 150.37 158.93 320.69 236.38 104.96 238.88 241.06 239.27 误差 0.69 0.52 −0.14 0.86 1.37 −0.86 0.15 0.93 0.04 0.40
下载: 导出CSV
表 4 耦合前地下水流模型均衡表（单位：104 m3）
Table 4. Equalization table of groundwater flow model before coupling (unit: 104 m3)
项 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 流入 河流 6.00 5.39 5.42 3.96 4.46 4.47 4.05 4.44 5.06 4.90 4.19 5.15 5.28 4.61 降雨 95.51 106.89 99.73 132.19 105.53 109.14 141.48 80.55 94.97 119.34 105.56 77.89 105.85 101.00 总流入 101.51 112.28 105.15 136.15 109.99 113.61 145.53 84.99 100.03 124.24 109.76 83.04 111.14 105.60 流出 边界 36.60 36.50 36.5 36.50 36.60 36.50 36.50 36.50 36.60 36.50 36.50 36.50 36.50 36.50 河流 60.57 65.39 64.70 84.31 76.81 75.97 85.22 79.15 67.58 68.91 80.96 65.22 64.40 72.41 蒸发 0.34 0.37 0.36 0.49 0.44 0.43 0.49 0.45 0.37 0.38 0.46 0.36 0.36 0.41 总流出 97.51 102.26 101.57 121.30 113.85 112.90 122.21 116.10 104.55 105.80 117.92 102.08 101.36 109.32 均衡 4.00 10.02 3.58 14.85 −3.86 0.71 23.32 −31.11 −4.52 18.44 −8.16 −19.05 9.77 −3.71 总均衡 14.28
下载: 导出CSV
表 5 耦合后地下水流模型均衡表（单位：104m3）
Table 5. Equilibrium table of groundwater flow model after coupling (unit: 104m3)
项 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 流入 河流 0.75 0.99 0.76 0.70 0.57 0.65 0.64 0.43 0.70 0.93 0.54 0.72 1.11 0.78 降雨 102.80 109.61 87.05 214.65 135.54 141.00 209.76 74.45 80.33 160.17 116.36 52.15 125.39 118.29 总流入 103.54 110.59 87.82 215.35 136.12 141.65 210.39 74.88 81.02 161.1 116.90 52.87 126.50 119.07 流出 边界 36.60 36.5 36.50 36.50 36.60 36.50 36.50 36.50 36.60 36.50 36.50 36.50 36.60 36.50 河流 81.98 59.20 71.96 117.54 101.81 100.52 118.00 107.79 70.73 70.99 107.99 60.90 55.20 82.76 蒸发 1.05 0.66 1.10 1.92 1.50 1.57 1.61 1.83 0.99 0.89 1.82 0.81 0.68 1.23 总流出 119.62 96.36 109.57 155.96 139.91 138.58 156.11 146.12 108.32 108.38 145.73 98.21 92.49 120.49 均衡 −16.08 14.24 −21.75 59.39 −3.80 3.06 54.28 −71.24 −27.29 52.72 −28.82 −45.34 34.01 −1.42 总均衡 1.96
下载: 导出CSV
-
[1] 闫红飞, 王船海, 文鹏. 分布式水文模型研究综述[J]. 水电能源科学, 2008, 26(6):1-4. doi: 10.3969/j.issn.1000-7709.2008.06.001YAN Hongfei, WANG Chuanhai, WEN Peng. Overview of studies on distributed hydrological model[J]. Water Resources and Power, 2008, 26(6):1-4. doi: 10.3969/j.issn.1000-7709.2008.06.001 [2] 吕清华. SWAT模型对农业面源污染模拟的适用性分析[J]. 云南水力发电, 2022, 38(2):57-59. doi: 10.3969/j.issn.1006-3951.2022.02.013LV Qinghua. Applicability analysis of SWAT model to agricultural non-point source pollution simulation[J]. Yunnan Water Power, 2022, 38(2):57-59. doi: 10.3969/j.issn.1006-3951.2022.02.013 [3] Saha G K, Cibin R, Elliott H A, Elliott H A, Preisendanz H E. Toward a robust land suitability framework for manure management: Modeling impacts and evaluating biophysical characteristics[J]. Journal of the American Water Resources Association, 2022, 58(3): 435-452. [4] 魏健, 潘兴瑶, 孔刚, 白涛, 黄强, 李波, 马盼盼. 基于生态补水的缺水河流生态修复研究[J]. 水资源与水工程学报, 2020, 31(1):64-69, 76.WEI Jian, PAN Xingyao, KONG Gang, BAI Tao, HUANG Qiang, LI Bo, MA Panpan. Study on ecological restoration of water-deficient rivers based on ecological water supplement method[J]. Journal of Water Resources and Water Engineering, 2020, 31(1):64-69, 76. [5] 陈栋, 梁敏, 仇春光, 王颖聪, 蒋坤. 基于水质模拟分析的生态补水方案研究[J]. 人民长江, 2018, 49(Suppl.1):34-37.CHEN Dong, LIANG Min, CHOU Chunguang, WANG Yingcong, JIANG Kun. Ecological water supplement solution based on water quality simulation[J]. Yangtze River, 2018, 49(Suppl.1):34-37. [6] 焦丽君, 刘瑞民, 王林芳, 党晋华, 肖艳艳, 夏星辉. 基于SWAT模型的汾河流域生态补水研究[J]. 生态学报, 2022, 42(14): 5778-5788JIAO Lijun, LIU Ruimin, WANG Linfang, DANG Jinhua, XIAO Yanyan, XIA Xinghui. Study on ecological water supplement in Fenhe river basin based on SWAT model[J]. Acta Ecologica Sinica, 2022, 42(14): 5778-5788. [7] 卜玉. 基于SWAT模型的中长期洪水径流预测研究[J]. 黑龙江水利科技, 2022, 50(4): 165-168, 224.PU Yu. Study on medium and long term flood runoff prediction based on SWAT model[J]. Heilongjiang Hydraulic Science and Technology, 2022, 50(4): 165-168, 224. [8] Sushanth K, Sandeep H, Rao B K. Assessment of inflows to Rallapadu reservoir from catchment area using SWAT Model[J]. Indian Journal of Ecology, 2020, 47(11). [9] 刘家威, 蔡宏, 郑婷婷, 唐敏. 基于SWAT模型的赤水河流域径流年内分配特征及其对降水的响应研究[J]. 水土保持通报, 2022, 42(3):180-187. doi: 10.3969/j.issn.1000-288X.2022.3.stbctb202203024LIU Jiawei, CAI Hong, ZHENG Tingting, TANG Min. Annual distribution characteristics of Chishui river watershed runoff and its response to precipitation based on SWAT model[J]. Bulletin of Soil and Water Conservation, 2022, 42(3):180-187. doi: 10.3969/j.issn.1000-288X.2022.3.stbctb202203024 [10] 邰理想, 饶文波, 檀涛, 谭红兵, 姜三元, 张西营. 基于格尔木河流域的SWAT模型水文特征情景模拟研究[J]. 水文, 2023, 43(2): 46-51.TAI Lixiang, RAO Wenbo, TAN Tao, TAN Hongbin, JIANG Sanyuan, ZHANG Xiying. Scenario simulation research on hydrological characteristics of the Golmud river basin based on SWAT model[J]. Journal of China Hydrology, 2023, 43(2): 46-51. [11] Luo Z, Shao Q. A modified hydrologic model for examining the capability of global gridded PET products in improving hydrological simulation accuracy of surface runoff, streamflow and baseflow[J]. Journal of Hydrology, 2022:127960. [12] Khadka A. Runoff modeling using SWAT Model in Little Wabash river watershed, Illinois[D]. Edwardsville, USA: Southern Illinois University at Edwardsville, 2022. [13] 胡倩, 王军霞, 刘世强, 吴嘉铃, 唐仲华, 成建梅. 基于SWAT模型的洞庭湖平原水资源量计算[J]. 安全与环境工程, 2022, 29(3):244-252. doi: 10.13578/j.cnki.issn.1671-1556.20210444HU Qian, WANG Junxia, LIU Shiqiang, WU Jialing, TANG Zhonghua, CHENG Jianmei. Calculation of water resources in Dongting lake plain based on SWAT model[J]. Safety and Environmental Engineering, 2022, 29(3):244-252. doi: 10.13578/j.cnki.issn.1671-1556.20210444 [14] 陈沛源, 李金文, 俞巧. 基于 SWAT 模型的泾河流域地下水分布特征与水资源评价[J]. 灌溉排水学报, 2021, 40(12):102-109, 126.CHEN Peiyuan, LI Jinwen, YU Qiao. Evaluation groundwater resource and its distribution in Jinghe basin using the SWAT model[J]. Journal of Irrigation and Drainage, 2021, 40(12):102-109, 126. [15] 孙振权, 魏涛, 洪梅. 基于SWAT模型的最佳管理措施对伊逊河流域水沙的影响研究[J]. 世界地质, 2022, 41(4): 914-925.SUN Zhenquan, WEI Tao, HONG Mei. Impact of best management practices on water and sediment in Yixun river basin based on SWAT model[J]. Global Geology, 2022, 41(4): 914-925. [16] 曹灿, 孙瑞, 吴志祥, 李茜. 基于SWAT模型的南渡江流域土地利用/覆被变化的径流响应[J]. 水土保持研究, 2022, 29(4):167-175. doi: 10.3969/j.issn.1005-3409.2022.4.stbcyj202204024CAO Can, SUN Rui, WU Zhixiang, LI Xi. Responses of streamflow to land use/cover changes in Nandu river basin based on SWAT model[J]. Research of Soil and Water Conservation, 2022, 29(4):167-175. doi: 10.3969/j.issn.1005-3409.2022.4.stbcyj202204024 [17] 严芳芳. Visual Modflow在水资源论证中的应用探讨[J]. 山东水利, 2021(5):44-45.YAN Fangfang. The discussion on the application of Visual Modflow in water resources argumentation[J]. Shandong Water Resources, 2021(5):44-45. [18] 温海燕, 吕昊楠. 基于Visual MODFLOW的丰南区北刘堼水源地地下水位预测[J]. 河南科技, 2021, 40(20):13-15. doi: 10.3969/j.issn.1003-5168.2021.20.013WEN Haiyan, LV Haonan. Groundwater level prediction of the Beiliuheng water source area in Fengnan district based on Visual MODFLOW[J]. Henan Science Technology, 2021, 40(20):13-15. doi: 10.3969/j.issn.1003-5168.2021.20.013 [19] 于红梅, 张楠, 燕艳, 李莉莉. 基于ModFlow对地下水资源量的计算[J]. 内蒙古水利, 2018(5):50-51. [20] Mondal N C, Singh V S. Mass transport modeling of an industrial belt using Visual MODFLOW and MODPATH: A case study[J]. Journal of Geography and Regional Planning, 2009, 2(1):1-19. [21] 何浩, 张强, 张金林, 冯杰, 李威龙, 王志鹏. 基于Visual Modflow研究武隆–广杨深层岩溶水径流特征[J]. 甘肃水利水电技术, 2022, 58(2):22-27, 34. [22] 赵良杰, 夏日元, 杨杨, 邵景力, 易连兴, 王喆. 基于MODFLOW的岩溶管道水流模拟方法探讨与应用[J]. 中国岩溶, 2017, 36(3):346-351. doi: 10.11932/karst20170308ZHAO Liangjie, XIA Riyuan, YANG Yang, SHAO Jingli, YI Lianxing, WANG Zhe. Discussion and application of simulation methods for karst conduit flow based on MODFLOW[J]. Carsologica Sinica, 2017, 36(3):346-351. doi: 10.11932/karst20170308 [23] 杨杨, 唐建生, 苏春田, 潘晓东, 赵良杰. 岩溶区多重介质水流模型研究进展[J]. 中国岩溶, 2014, 33(4):419-424. doi: 10.11932/karst20140405YANG Yang, TANG Jiansheng, SU Chuntian, PAN Xiaodong, ZHAO Liangjie. Research advances on multi-medium flow model for karst aquifers[J]. Carsologica Sinica, 2014, 33(4):419-424. doi: 10.11932/karst20140405 [24] 杨郑秋, 杨杨, 邵景力, 苏春田, 崔亚莉, 罗飞. 基于MODFLOW-CFP的岩溶水模型降雨非线性入渗补给研究:以湖南省香花岭地区为例[J]. 中国岩溶, 2019, 38(5):691-695.YANG Zhengqiu, YANG Yang, SHAO Jingli, SU Chuntian, CUI Yali, LUO Fei. Study on non-linear rainfall infiltration recharge of numerical karst water model based on MODFLOW-CFP: A case study of Xianghualing area, Hunan Province[J]. Carsologica Sinica, 2019, 38(5):691-695. [25] 李星宇, 南天, 王新娟, 李鹏, 谢振华, 邵景力. 数值模拟方法在隐伏岩溶水源地保护区划分及污染治理中的应用[J]. 中国岩溶, 2014, 33(3):280-287. doi: 10.11932/zgyr20140303LI Xingyu, NAN Tian, WANG Xinjuan, LI Peng, XIE Zhenhua, SHAO Jingli. Application of the numerical simulation method in concealed karst wellhead for protection area delimitation and contamination prevention[J]. Carsologica Sinica, 2014, 33(3):280-287. doi: 10.11932/zgyr20140303 [26] 杨杨, 赵良杰, 夏日元, 王莹. 珠江流域岩溶地下河分布特征与影响因素研究[J]. 中国岩溶, 2022, 41(4): 562-576.YANG Yang, ZHAO Liangjie, XIA Riyuan, WANG Ying. Distribution and influencing factors of karst underground rivers in the Pearl River Basin[J]. Carsologica Sinica, 2022, 41(4): 562-576. [27] 杨杨, 赵良杰, 潘晓东, 夏日元, 曹建文. 西南岩溶山区地下水资源评价方法对比研究:以寨底地下河流域为例[J]. 中国岩溶, 2022, 41(1):111-123.YANG Yang, ZHAO Liangjie, PAN Xiaodong, XIA Riyuan, CAO Jianwen. Comparative study on evaluation methods of groundwater resources in karst area of Southwest China: Taking Zhaidi underground river basin as an example[J]. Carsologica Sinica, 2022, 41(1):111-123. [28] 徐中平, 周训, 崔相飞, 拓明明, 王昕昀, 张颖. 岩溶区地下水数值模拟研究进展[J]. 中国岩溶, 2018, 37(4):475-483.XU Zhongping, ZHOU Xun, CUI Xiangfei, TUO Mingming, WANG Xinyun, ZHANG Ying. Research advances of numerical simulation of groundwater in karst areas[J]. Carsologica Sinica, 2018, 37(4):475-483. [29] 姜光辉. 融合生态学和提升岩溶水数值模拟技术的国际前沿研究[J]. 中国岩溶, 2016, 35(1):1-4. doi: 10.11932/karst201601y01JIANG Guanghui. The research progress and developing tendency of karst water[J]. Carsologica Sinica, 2016, 35(1):1-4. doi: 10.11932/karst201601y01 [30] 张琳琳, 崔亚莉, 梁桂星, 梁灵君, 王晓阳. SWAT-MODFLOW耦合模型在地下水量均衡分析中的应用[J]. 南水北调与水利科技(中英文), 2020, 18(6): 176-183.ZHANG Linlin, CUI Yali, LIANG Guixing, LIANG Lingjun, WANG Xiaoyang. Application of SWAT-MODFLOW coupling model in groundwater balance analysis[J]. South-to-North Water Transfers and Water Science & Technology, 2020, 18(6): 176-183. [31] Yifru B A, Chung I M, Kim M G, Chang S W. Assessing the effect of land/use land cover and climate change on water yield and groundwater recharge in East African Rift Valley using integrated model[J]. Journal of Hydrology: Regional Studies, 2021, 37:100926. doi: 10.1016/j.ejrh.2021.100926 [32] 王蕾. 基于SWAT-MODFLOW的变化环境下渠井结合灌区地下水循环特征研究[D]. 杨凌: 西北农林科技大学, 2017.WANG Lei. Study on characteristics of groundwater circulation in canal-well combined irrigation area under changing environment based on SWAT-MODFLOW model[D]. Yangling: Northwest A & F University, 2017. [33] 吴德丰. 基于SWAT-MODFLOW的灌区土壤水与地下水转化特征研究[D]. 郑州: 华北水利水电大学, 2021.WU Defeng. Assessment of water exchange between soil water and groundwater in irrigation area based on SWAT-MODFLOW[D]. Zhengzhou: North China University of Water Resources and Electric Power, 2021. [34] 周铮. 基于SWAT-MODFLOW模型的北山水库流域地表–地下水耦合模拟研究[D]. 南京: 南京大学, 2021.ZHOU Zheng. Coupling simulation of surface water and groundwater in Beishan reservoir watershed based on SWAT-MODFLOW[D]. Nanjing: Nanjing University, 2021. [35] Jafari T, Kiem A S, Javadi S, Nakamura T, Nishida K. Using insights from water isotopes to improve simulation of surface water-groundwater interactions[J]. Science of the Total Environment, 2021, 798:149253. doi: 10.1016/j.scitotenv.2021.149253 [36] Bailey R T, Wible T C, Arabi M, Records R M, Ditty J. Assessing regional-scale spatio-temporal patterns of groundwater-surface water interactions using a coupled SWAT-MODFLOW model[J]. Hydrological Processes, 2016, 30(23):4420-4433. [37] 康燕楠. 基于SWAT-MODFLOW的多尺度干旱时段水资源优化配置[D]. 杨凌: 西北农林科技大学, 2021.KANG Yannan. Multi-scale optimal allocation of water resources in drought periods based on SWAT-MODFLOW[D]. Yangling: Northwest A & F University, 2021. [38] Petpongpan C, Ekkawatpanit C, Bailey R T, Kositgittiwong D. Improving integrated surface water-groundwater modelling with groundwater extraction for water management[J]. Hydrological Sciences Journal, 2021, 66(10):1513-1530. doi: 10.1080/02626667.2021.1948549 [39] 张洪波, 支童, 卫星辰, 党池恒, 夏岩, 高文冰. 基于SWAT-MODFLOW的黄河中游区径流过程模拟及对黄土高原变绿的响应[J]. 华北水利水电大学学报(自然科学版), 2020, 41(6):1-10.ZHANG Hongbo, ZHI Tong, WEI Xingchen, DANG Chiheng, XIA Yan, GAO Wenbing. Simulation of runoff process in the middle Yellow River based on SWAT-MODFLOW and its response to the greening of the Loess Plateau[J]. Journal of North China University of Water Resources and Electric Power (Natural Science Edition), 2020, 41(6):1-10. [40] Frederiksen R R, Molina Navarro E. The importance of subsurface drainage on model performance and water balance in an agricultural catchment using SWAT and SWAT-MODFLOW[J]. Agricultural Water Management, 2021, 255:107058. doi: 10.1016/j.agwat.2021.107058 [41] Bailey R, Rathjens H, Bieger K, Chaubey I, Arnold J. SWATMOD-Prep: Graphical user interface for preparing coupled SWAT-MODFLOW simulations[J]. JAWRA Journal of the American Water Resources Association, 2017, 53(2):400-410. doi: 10.1111/1752-1688.12502 [42] Bosch D D, Sheridan J M, Lowrance R R, Hubbard R K, Strickland T C, Feyereisen G W, Sullivan D G. Little river experimental watershed database[J]. Water Resources Research, 2007, 43(9): W09470.1-W09470.6. 期刊类型引用(5)
1. 杨蕴，郭勇，王发飞，宋健，吴剑锋. 山谷型小流域地表水与地下水时空交互模拟研究. 水文地质工程地质. 2025(01): 32-41 . 
百度学术2. 王美悦，李旭，杨克娟，杨秉阳. 凹山矿坑地下水动态特征与数值模拟研究. 地下水. 2025(01): 80-83 . 百度学术3. 高琪，王海芳，吕溥，李金惠，李鑫. 泰兴市非饱和带与饱和带间固液界面传质模型的推导. 环境保护科学. 2024(02): 154-160 . 百度学术4. 杨丽，杨广斌，李亦秋，李蔓. 修正SWAT模型在喀斯特小流域的径流模拟研究——以羊鸡冲小流域为例. 中国岩溶. 2024(02): 291-301 . 
本站查看5. 高岩. 地表水中温度、溶解氧和氨氮的关系研究——以广州海珠区为例. 生态与资源. 2024(07): 16-18 . 百度学术其他类型引用(4)
-
下载:
百度学术
点击查看大图
计量
- 文章访问数: 557
- HTML浏览量: 90
- PDF下载量: 181
- 被引次数: 9
